Encore un inventaire à la Prévert ? Non, pas tout-à-fait en tout cas. Plutôt moins que pourrait y ressembler le rapprochement de ces dates lues dans la presse d’avant-hier 14 mars 2018 :
15 février 1564 : Naissance de Galilée.
14 mars 1879 : Naissance d’Albert Einstein.
14 mars 2018 : Décès de Stephen Hawking.
Alors, pourquoi ce titre ? D’abord parce qu’il valait bien à mes yeux celui retenu par Le Figaro d’hier matin 15 mars 2018 :

La vraie superstar de la physique demeure pour moi encore Albert Einstein. Celui qui est l’auteur de la plus célèbre formulation mathématique d’une loi physique : E = mc2 . Une formule connue d’une foule de gens, mais dont véritablement très peu d’entre eux sont capables d’en expliciter la signification.
Ce sens, j’ai fait le choix de l’évoquer dans mon titre en associant à Stephen Hawking celui du superbe livre de Richard Feynman (une autre star de la physique) : « Lumière et matière ». La lumière, ce sont les photons, ces particules élémentaires dépourvues de masse, toutes entières énergie, jamais à l’arrêt, et pour toujours animées d’une vitesse insurpassable, ce c de la formule d’Einstein. Et des photons, Hawking en a fait les partenaires omniprésents de ses intuitions géniales et des théories physiques révolutionnaires qui ont fait sa célébrité.
Après « Lumière et matière », le second attribut qui m’est venu sous la plume pour évoquer la vie et l’œuvre de Stephen Hawking, c’est « L’Everest ». Parce que les 8848 m auxquels culmine cette montagne symbolisent de la façon la plus saisissante qui soit, la quête d’un but pratiquement inatteignable, ou alors seulement au prix d’efforts dépassant ce qui se peut ordinairement concevoir. Et là, le cinéma m’a aidé, avec la diffusion le 11 mars dernier, il y a donc moins d’une semaine, du film justement intitulé « Everest », qui retrace le drame ayant causé le 10 mai 1996 la mort de huit alpinistes chevronnés. Aujourd’hui, parmi les 14 000 personnes qu’ils l’ont tenté, seules 4000 ont réussi à aller au bout de l’ascension de l’Everest et le plus souvent à relever le défi d’une vie. Et quelques 800 y ont perdu cette vie. C’est pourquoi cette ascension de l’Everest est tout simplement mythique et peut symboliser aujourd’hui la quête d’un but presque inaccessible .

Cette quête d’un but presque inaccessible, c’est encore le cinéma qui m’en a offert un bel exemple, avec le film de James Marsh « Une merveilleuse histoire du temps » qui retrace d’une manière si émouvante l’histoire de ce jeune et brillant étudiant confronté soudain à l’annonce d’une mort prochaine, paralysé par la maladie de Charcot (sclérose latérale amyotrophique) qui l’atteint à l’age de 21 ans. Hawking ne va bientôt plus pouvoir ni bouger ni parler; il devra communiquer grâce à un dispositif lui permettant de sélectionner des mots sur un écran par une légère contraction de la joue et un rayon infrarouge attaché à ses lunettes, mots prononcés ensuite par un synthétiseur vocal. Et pourtant, il va poursuivre sans relâche son activité intellectuelle, jusqu’à l’age – incroyable pour ses médecins – de 76 ans (Le même que celui de Galilée !). Il vient, en ayant relevé avec succès le défi que lui imposait la maladie, de conquérir ainsi son Himalaya à lui.

Le troisième attribut – les trous noirs – s’imposait également, tant ces objets physiques désormais omniprésents en cosmologie ont focalisé la réflexion de Hawking , lequel a ainsi contribué puissamment à la naissance d’une nouvelle physique. Hawking a ainsi montré que les trous noirs ne l’étaient pas complètement, qu’ils émettaient un flux de particules aujourd’hui universellement connu sous le nom de rayonnement Hawking et le spectre de ce rayonnement était précisément celui de Planck. Un résultat prodigieux montrant la cohérence incroyable des lois de la physique.
Mais les trous noirs, cela allait vite devenir aussi mon Everest à moi. Car la compréhension de leur physique supposait d’abord d’acquérir celle de la Relativité Générale. Un sommet vertigineux ! Et s’il n’y avait eu que moi dans l’aventure encore… Mais j’emmenai avec moi une cordée de douze aventuriers seniors de l’Université Tous Ages de Vannes. Et s’ils allaient poser le sac et faire demi-tour avant le sommet ?
Le planning de ce parcours un brin insensé était prévu pour une durée de 18 semaines ; La préparation initiale avait, vous vous en doutez, une importance capitale. C’est pourquoi l’acclimatation aux tenseurs, un danger redoutable à l’altitude de la Relativité Générale, exigea pas moins de 8 semaines au Camp de base N°1. Voici une image qui vous donnera une vague, très vague idée des dangers encourus, et des techniques à assimiler pour demeurer en sécurité :

Mais après tous ces efforts, jugez de l’explosion de joie qui envahit le groupe lorsqu’il put enfin percevoir dans son champ de vision, le magnifique spectacle offert par les 10 équations d’Einstein qui s’offraient à leur regard :

Assurément le sommet n’était plus loin ! Je savais que devant nous s’ouvrait la voie dite du tenseur covariant de Ricci :
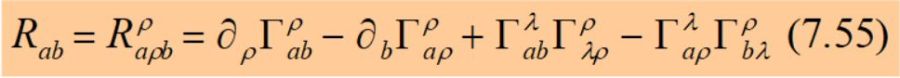
ce qui nous conduisit enfin vers ce à quoi nous aspirions depuis si longtemps, une solution exacte des équations de Einstein :
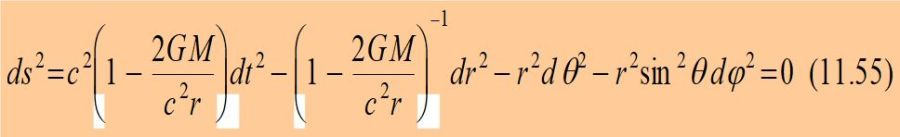
Cette solution est connue sous le nom de métrique de Schwarzschild. Elle permet d’étudier la physique au voisinage d’un corps de masse M, et en particulier les trajectoires de particules massives en chute libre ou les trajectoires de photons.
Et c’est là que nous rejoignons les premiers travaux de Stephen Hawking quand il soutenait sa thèse de doctorat en physique à Cambridge. Cette solution a comme particularité de faire apparaître une singularité lorsque la variable d’espace r tend vers la valeur 2GM/c2 (Une longueur appelée le rayon de Schwarzschild).
Cette singularité physique de l’espace-temps décrit le cas du phénomène d’effondrement sur elle-même d’une étoile de très forte masse, ce qui conduit alors à la formation d’un trou noir de Schwarzschild.
Voilà. Nous en resterons là. Sachez juste que ce billet d’aujourd’hui se trouve être le numéro 100 d’une série débutée le 19 mars 2011 à la suite de la nouvelle subite dans les media de la catastrophe de Fukushima au Japon. Ce blog naquit donc avec le déchaînement de l’océan Pacifique et de l’énorme tsunami qui provoqua la mort de 20 000 personnes et la destruction de la centrale nucléaire de Fukushima. Et cette série de 100 billets se termine avec la disparition du plus étonnant scientifique de ce début de 21ème siècle, pratiquement 140 ans jour pour jour après la naissance de son plus illustre prédécesseur dans l’Olympe des physiciens, Albert Einstein.
En guise d’annexe, je donne ci-dessous le sommaire du cours que j’ai enseigné du 2 octobre 2013 au 16 avril 2014, à l’Université Tous Ages (U.T.A) de Vannes :
Relativité Générale et Cosmologie
I – Introduction à la cosmologie
II – Premiers éléments de calcul tensoriel
III – Compléments sur le calcul tensoriel
IV – La relativité restreinte (Première partie)
V – La relativité restreinte (Seconde partie)
VI – Vers la relativité généralisée
VII – Courbure de l’Espace-temps : Les symboles de Christoffel
VIII – Courbure de l’Espace-temps : Le tenseur de Riemann
IX – Les fondements de la relativité générale
X – Les équations du champ de gravitation d’Einstein
XI – Solution de Schwarzschild pour un champ central à symétrie sphérique
XII – Les vérifications expérimentales de la théorie de la relativité générale
XIII – Les premiers pas de la cosmologie
XIV – Équations de Friedmann-Lemaître comme solution des équations d’Einstein
XV – Paramétrisation des modèles cosmologiques de Friedmann-Lemaître
XVI – Comparaisons entre les divers modèles FLRW et les observations
XVII – Le modèle du Big Bang de Friedmann – Lemaître et le rayonnement cosmique fossile
XVIII – Vers la cosmologie du XXIe siècle. Le modèle de l’inflation
Et voici la liste (par ordre alphabétique) des courageux étudiants du troisième âge qui n’hésitèrent pas à me suivre pendant l’année universitaire 2013-2014, afin de suivre un cours en dix-huit séances de 2 heures, dont l’objectif, pour le moins téméraire, était de comprendre en en refaisant tous les calculs, l’établissement des équations d’Einstein de la relativité générale, puis ensuite d’appliquer ces résultats à l’analyse détaillée des modèles cosmologiques qui ont conduit à la théorie improprement baptisée du nom de Big Bang.
Voici donc les noms de ces 18 vaillants étudiants qui ont chacun conquis leur propre Everest en maîtrisant l’essentiel de la théorie de la relativité générale :
Jean-Michel Bernard ; Franklin Boisnet ; Olivier Cadel ; Yves Casadepax ; Paul Clementi ; Xavier Denis ; Alain Fisch ; Jean-Marie Hartmann ; Dominique Laurans ; Dominique Le Mene ; Armelle Le Saux ; Patrice Mallet ; Michel Bernard ; Catherine Marly ; Michel Piacentino ; Ursula Scrizzi ; Françoise Valentin ; Michel Vanvaerenbergh .
