Les règles de confinement qui ont été récemment appliquées à la société française ont déjà une multitude de conséquences, grandes ou petites. Parmi les petites, les plus petites sans doute, on peut citer celle qui fut de couper les ailes à une initiative fort intéressante intitulée « Club de physique de l’Université Tous Ages de Vannes ».
Pour plus de clarté, voici le court texte qu’on peut considérer comme l’acte de naissance de cette institution :
« Ce Club, gratuit pour les adhérents à l’UTA, vient de se créer. Il est organisé autour d’anciens élèves fidèles des Cours de Physique donnés à l’UTA pendant une dizaine d’années. Le principe consistera pour chaque membre volontaire à approfondir un point de Physique de son choix, se l’approprier, le présenter, le partager ensuite dans ses propres mots avec les autres. À priori l’approche de ces présentations serait plus pragmatique, pratique même, que mathématique. Le Club se réunira dans une salle de l’UTA, tous les deuxièmes mercredis du mois, de 10 à 12 heures, à compter du 9 octobre 2019 »
Rappelons brièvement quelles furent les activités du Club d’octobre 2019 à février 2020. Les deux premières séances, en octobre et novembre 2019 furent consacrées à l’apprentissage d’un exercice intellectuel peu commun de nos jours, consistant à déterminer l’heure de la marée sans montre ni calculette ni tables ! Puis décembre 2019 nous vit effectuer une instructive ballade expérimentale à travers les effets des champs électromagnétiques. En janvier 2020, ce fut une évocation des premiers grands travaux en cosmologie, et en février 2020, le Club s’en fut à la découverte des grands mécanismes à l’origine des courants océaniques.
La séance de mars devait être consacrée à la découverte de 10 grandes idées pour bien comprendre les bases scientifiques de la prévision météorologique. Hélas, le coronavirus allait en décider autrement. Nous allons donc faire autrement. Aujourd’hui, vous aller trouver ci-dessous une première partie de la présentation que je devais faire au Club. Vous réagissez via le canal des commentaires, auxquels je réponds si des questions étaient posées. Puis je poste sur le blog la suite de la présentation, et ainsi de suite. Seule différence, mais très intéressante : Le club n’est pas fermé, mais au contraire ouvert à tous les internautes qui connaissaient déjà le blog, et à ceux qui vont éventuellement le découvrir. Bonne lecture l

Le dictionnaire « Le Robert » nous apprend que « La météorologie est l’étude scientifique des phénomènes atmosphériques », le terme ‘ Météorologie ‘ venant du grec meteôros ( ‘qui est en haut ‘).
Vue de l’espace, la limite de l’atmosphère ressemble à un fin halo de lumière bleu foncé sur un horizon en forme de courbe.
L’atmosphère est si mince qu’on peut se représenter son épaisseur relativement à la Terre comme la pelure d’une pomme relativement à l’ensemble du fruit. C’est la force d’attraction de la Terre qui retient l’atmosphère autour du globe.

Cette atmosphère est un mélange gazeux qui contient également un certain nombre d ’autres constituants permanents en proportions très faibles, mais très variables .

Mais tout se complique car l’air atmosphérique contient toujours en plus une quantité variable de vapeur d’eau . Cette vapeur d’eau provient de l’évaporation des océans, ce processus empruntant à ces océans des quantités importantes de chaleur . Toute cette énergie sera libérée ultérieurement dans l’atmosphère, lors des phénomènes de condensation de la vapeur d’eau. L’humidité de l’air se retrouvera alors sous forme liquide ou solide, sous forme de nuages. Des précipitations sous forme de pluies, grêles et neiges pourront alors refermer ce cycle de l’eau dans l’atmosphère .

Comprendre la météorologie, c’est donc se familiariser avec la description physique du comportement de l’énorme masse gazeuse enveloppant notre planète, que l’on peut décrire ainsi : Une mince couche fluide d’une dizaine de km d’épaisseur, constituée en première approximation d’un mélange de gaz (l’air sec), air sec dans lequel il faudra ensuite prendre en compte la présence d’eau ( C’est-à-dire d’un milieu mille fois plus dense, et aux propriétés thermiques bien différentes ) .
Commençons par nous occuper de l’air sec, et de son équilibre dit hydrostatique (l’état de repos).
Le premier paramètre à prendre en compte est la pression atmosphérique au sol p.a0, c’est-à-dire la force exercée verticalement sur une surface de sol de un mètre carré par la colonne d’air de hauteur H qui surmonte cette surface :

Le volume V de cette colonne d’air est : V = H . 1 m2 = H m3
La masse totale d’air sec contenue dan la colonne est : m = ρ V = ρ H ,
ρ étant la masse par unité de volume de l’air sec.
Le poids total d’air sec P dans le volume V est alors donné par :
P = m g = ρ g H Newton,
g étant l’accélération de la pesanteur donnée par :
g = 9,81 m/s2 et le Newton étant l’unité légale de force.
Attention ! Ne confondez surtout pas masse et force !
La masse est une caractéristique fondamentale de la matière qui s’exprime en kilogrammes.
Le poids est une caractéristique d’un objet, d’un corps, qui s’exprime en Newton. C’est une force due à la pesanteur, mesurée par le coefficient g ci-dessus. Sur la lune, un corps aura ainsi un poids plus faible que sur la Terre. Dans le vide de l’espace, ce corps ne pèsera plus rien, mais il aura toujours la même masse.
On peut immédiatement donner une première approximation de la pression atmosphérique p.a0 au sol : c’est le poids P de la colonne d’air qui appuie sur la surface unité :
p.a0 = P / 1 m2 = ρ g H Pascal (Pa) = 1 kg/m3 x 9,8 m/s2 x 10.000 m
soit : p.a0 ≈ 100 000 Pa
en prenant : H = 10 000 m, ρ = 1 kg/m3 , et en se souvenant que l’unité légale de pression est le Pascal (Pa) :
1 Pa = 1 Newton par m2.
Le Pascal est une unité relativement petite. C’est pourquoi en météorologie, on préférera un multiple du Pascal, 100 fois plus grand, l’hectoPascal, en abrégé hPa :
1 hPa = 100 Pa, et par conséquent :
La pression atmosphérique vaudra approximativement : p.a0 ≈ 1000 hPa
Une autre unité de pression est encore utilisée : le bar.
Par définition: 1 bar = 100 000 Pa et 1 millibar (mPa) = 100 Pa,
d’où : p.a0 ≈ 1000 mbar
Mais c’est oublier que la température T de l’atmosphère varie avec l’altitude z . Comme l’air est compressible, sa masse volumique est donc une fonction décroissante de la température en fonction de z . Il s’en suit que la pression atmosphérique p à une altitude z quelconque, est également une fonction p(z) devant respecter la condition hydrostatique :
(1) dp = – ρ(z) g dz
Cette équation n’est qu’un moyen commode et peu encombrant pour dire la chose suivante :
Quand on part d’une altitude z et qu’on descend en altitude d’une hauteur dz (en mètres), la grandeur positive – dz exprime en mètres cubes la quantité dont a augmenté la colonne d’air de base 1 m2 surmontant la cote de départ z. Et le produit de ce volume par la masse volumique ρ(z) est la quantité dont a augmenté la pression p(z), grandeur que l’on note dp .
Admirez donc l’efficacité du langage des équations, ce premier exemple vous montrant que ce sont alors trois lignes entières de discours que l’on remplace par un tout petit bout de ligne !
En postulant que l’air sec se comporte comme un gaz parfait, l’état thermodynamique d’une masse m de ce gaz dépend des trois paramètres suivants :
– sa pression p en Pascal
– sa température T en Kelvin
– son volume V en m3
Ces trois paramètres sont liés par l’équation d’état :
(2) p V = m Ra T
dans laquelle Ra est une constante spécifique de l’air sec :
Ra = 287 J/( kg . °K)
En introduisant m = ρ V dans la relation (2) , l’encombrant volume V disparaît et l’équation d’état de l’air sec s’écrira finalement :
(3) p(z) = ρ(z) Ra T(z)
En rapprochant alors cette relation (3) avec :
(1) dp = – ρ(z) g dz
on obtient :
On peut donc déjà être sûrs de deux grandes caractéristiques de l’atmosphère :
a) La pression atmosphérique p décroît quand on grimpe en altitude.
b) La température T décroît en même temps
On ne peut pas pour autant résoudre l’équation logarithmique (4). Les météorologistes ont donc contourné la difficulté en définissant un modèle standard aussi proche que possible de la réalité supposant une décroissance linéaire de la température en fonction de l’altitude, comme ceci :
Ce qui conduit finalement au modèle suivant d’atmosphère standard :
appelé modèle d’atmosphère standard OACI ( Organisation Internationale de l’Aviation Civile).
Il nous faut maintenant préciser les valeurs numériques à attribuer aux constantes p0 , T0 et k .
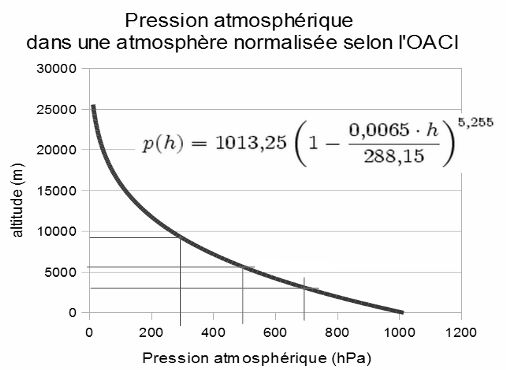
On a coutume de considérer p0 = 1013,25 hPa comme valeur « normale » de la pression atmosphérique au niveau z = 0 . (Cela correspond aux 76 cm de la colonne de mercure bien connus)
Le choix de T0 résulte de considérations que nous développerons un peu plus loin.
C’est : T0 = 15 °C
Quant au gradient de température k = dT/dz , il a été dicté par les observations et vaut :
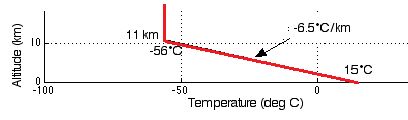
Ces deux lois de variation des caractéristiques essentielles de l’atmosphère en fonction de l’altitude z , loi (6) pour la pression atmosphérique p(z) , et loi (7) pour la température de l’air T(z) , vous seront décrites d’une manière plus parlante par les deux graphiques ci-dessous :
.
.
.
Il vous sera utile de mémoriser les 4 niveaux de pression atmosphérique p(z) suivants que nous retrouverons dans la suite de ces exposés :
.
300 hPa à 9100 m
500 hPa à 5500 m
700 hPa à 3000 m
850 hPa à 1500 m
.
Voilà. C’est assez pour ce première ‘ idée ‘ . Et n’oubliez pas de faire usage de la facilité dite des commentaires, pour poser toutes les questions qui pourraient vous aider à mieux comprendre tout ce qui précède. Les réponses seront données immédiatement sur ce blog.
À bientôt pour la « Deuxième grande idée ».









J’ai eu un problème de compréhension du passage suivant:
« On peut donc déjà être sûrs de deux grandes caractéristiques de l’atmosphère :
a) La pression atmosphérique p décroît quand on grimpe en altitude.
b) La température T décroît en même temps »
Et plus particulièrement avec le mot « donc »:
Je ne voyais pas comment la phrase (b) pouvait découler de ce qui précédait.
En lisant la suite j’ai ensuite compris que la formule (5) qui précise cette phrase (b) était en fait un choix empirique fondé sur l’expérience.
J’en fait l’interpretation suivante:
En adoptant cette formule on peut valablement modéliser les évolutions de température dans les mouvements de l’air sans s’occuper de la contribution de la conduction thermique et des émissions et absorption de rayonnement.
Est-ce bien exact?
Cher André,
Je reprends deux des équations fondamentales concernant la pression atmosphérique et la température T de l’air atmosphérique données dans le texte :
(1) dp = – ρ(z) g dz
Le signe – nous dit que la pression p décroît quand l’altitude z augmente. C’est mon point a)
a) La pression atmosphérique p décroît quand on grimpe en altitude.
(2) p V = m Ra T
Le volume V et le produit m Ra sont des grandeurs positives. Cela me montre que lorsque p décroît, il en est de même pour T. C’est mon point b)
b) La température T décroît en même temps
Voilà donc tout simplement pourquoi j’étais fondé à employer le ‘donc’ de mon affirmation :
» On peut donc déjà être sûrs de deux grandes caractéristiques de l’atmosphère :
a) La pression atmosphérique p décroît quand on grimpe en altitude.
b) La température T décroît en même temps . »
J’en viens maintenant à la seconde partie de votre question, qui concerne la relation (5) :
(5) T = T0 – k z
Cette linéarisation du profil de température ne repose en effet sur aucune autre loi physique. Elle est justifiée car elle ne contredit pas beaucoup les observations, mais a le grand avantage de permettre de calculer la solution p(z) (6) de l’équation différentielle ( 4).
Mais ceci ne fournit aucune information théorique permettant de calculer l’évolution de la température d’une masse d’air déterminée dans l’atmosphère. Par contre, je peux vous dire que les échanges conductifs sont vraiment de très peu d’importance, car l’air est un assez bon isolant thermique. Il conduit très peu la chaleur.
Le rayonnement non plus ne joue pas grand rôle dans les évolutions de la température.
Tout s’explique par les transports d’énergie convectifs entre masses d’air à des niveaux d’énergie différents,
et par les processus de vaporisation et de condensation capables de mobiliser de très grandes quantités d’énergie (la chaleur latente de vaporisation est grande). C’est donc l’humidité de l’atmosphère qui est un des arbitres de sa température.
Nous verrons cela plus tard avant dans les derniers billets de la série de 10.
Pierre Cormault
Mon trouble sur le « donc » n’est pas dissipé.
Il me semble en effet que p V = m Ra T est tout à fait compatible avec une décroissance de p et une croissance de T, il suffit en effet, pour m fixe, que V croisse plus vite que p ne décroit (toutes ces grandeurs étant positives).
D’ailleurs sur le deuxième schéma à la fin du texte, auquel je n’avais pas fait attention, on voit que, au-dessus de 11 km, T ne décroit plus, alors que p continue forcément à décroître.
Je vais donc dissiper votre trouble, définitivement j’espère.
Le premier sujet de trouble : comportement des grandeurs pV et m Ra T quand l’altitude z varie ?
Il s’agit de suivre le comportement d’une « petite portion d’atmosphère » quand son altitude va varier un peu. Dans les modèles météo on appelle cette portion une » parcelle » . Disons 1 mètre cube par exemple. La présence de V ne doit pas vous perturber. C’est pourquoi un peu plus loin dans le billet, vous pouvez lire :
» En introduisant m = ρ V dans la relation (2) , l’encombrant volume V disparaît et l’équation d’état de l’air sec s’écrira finalement :
(3) p(z) = ρ(z) Ra T(z)
En rapprochant alors cette relation (3) avec :
(1) dp = – ρ(z) g dz
on obtient :
(4) dp/p = – (g/Ra T) dz
relation dans laquelle l’absence de V doit vous tranquilliser et qui prouve bien que les variations dp et dz sont de signes contraires.
Quand z augmente (quand on monte), la pression p diminue, quoi qu’il arrive !
Second sujet : L’inversion de température qu’on constatera toujours en montant suffisamment haut ?
Soyez rassuré également. Ce phénomène s’appelle la tropopause. Cette inversion marque en fait la fin de l’atmosphère . Au-delà de cette frontière, on a quitté l’atmosphère. On n’est plus dans le champ d’observation concernant la météorologie. C’est précisément la première grande idée sujet de ce billet : La météorologie est la science qui analyse le comportement de l’atmosphère.
Au-delà de la tropopause, la pression p est voisine de 0 . Ce n’est plus un paramètre. On ne parle donc plus de météorologie.
Néanmoins, nous verrons plus loin, qu’il est d’un grand intérêt en météo de surveiller l’altitude très variable (disons entre 7000 et 11500 m) à laquelle on observe cette tropopause.