Dans les deux billets précédents, nous avons mis en avant deux grandes idées :
I – Interroger la météorologie, dans l’intention banale de savoir ‘ le temps qu’il va faire ? ‘, c’est essentiellement scruter l’atmosphère terrestre pour tenter de prévoir l’évolution dans le temps de deux paramètres fondamentaux : la pression atmosphérique et la température de cette atmosphère.
II – Nous avons identifié le moteur unique gouvernant les grandes évolutions dans l’espace et le temps de l’atmosphère terrestre. Il s’agit du rayonnement thermique dispensé par notre étoile, le Soleil, dont nous avons montré que l’énergie est reçue d’une manière inégale en fonction de la latitude et du moment dans le temps .
Nous sommes encore terriblement loin de pouvoir tenter de répondre à la question du temps qu’il va faire ! La troisième grande idée pour progresser dans la compréhension de la dynamique de l’atmosphère terrestre est la suivante :
La dynamique de l’atmosphère terrestre est soumise aux lois physiques gouvernant les phénomènes de rayonnement thermique
Quelles sont ces lois physiques ? Ce sont essentiellement celles résultant des travaux de Max Planck (1858-1947) et Albert Einstein (1879-1965), au début du XXème siècle, travaux qui nous ont fait comprendre les grands principes des interactions entre les rayonnements et la matière.
Le schéma ci-dessous nous montre qu’un rayonnement (c’est-à-dire une onde électromagnétique telle que la lumière visible, mais encore l’infrarouge, l’ultraviolet, les rayons X, etc.) frappant de la matière, peut être réfléchie par cette matière, et/ou traverser cette matière, et/ou encore être absorbée en totalité ou en partie par cette matière :
Chacun des trois coefficients, R pour la réflexion, A pour l’absorption, T pour la transmission, pourra prendre n’importe quelle valeur entre 0 et 100, en fonction des natures du rayonnement et de la matière, en respectant toutefois la condition de conservation I = R + A + T .
Lorsque l’on décompose la lumière blanche du Soleil à l’aide d’un prisme on observe un éventail de couleurs. On dit que la lumière blanche possède un spectre continu, car on passe d’une couleur à une autre sans interruption dans la succession des couleurs. Tout corps (gazeux ou solide) sous haute pression et à haute température (comme le Soleil), donne naissance à un spectre continu de lumière :
L’examen du spectre visible, illustré par le schéma ci-dessus, qui ne comporte aucune partie noire et brillante, rappelle que le noir est, plutôt qu’une couleur, une absence de couleur.
Les fenêtres ouvertes de cette façade ne laissent rien voir de la pièce qu’elles pourraient découvrir. Contrairement aux murs ou aux vitres des fenêtres fermées, qui réfléchissent la lumière incidente, elles renvoient très peu de lumière visible, ce qui explique leur aspect noir.
Les détecteurs optiques ont pour mission de rendre compte de l’information lumineuse. Cette opération nécessite l’absorption des photons. La pupille de l’œil humain, montre qu’elle apparaît noire. C’est un détecteur. Son aspect noir prouve que la pupille ne renvoie aucun des photons qu’elle reçoit (comme les fenêtres noires ci-dessus) . Ces deux analogies vont nous aider à comprendre la notion théorique de corps noir, précisée sur la figure suivante :
Une étoile comme le Soleil constitue un corps noir. A basse résolution spectrale, le spectre du soleil se superpose à celui d’un corps noir de température 5800 K (5777 K exactement). Et pourtant rien n’est moins noir que le soleil. Il apparaît donc nécessaire de donner une définition précise de ce qu’est un corps noir… qui peut être coloré.
Un corps noir est défini par l’équilibre intime entre sa matière et son rayonnement. Sa température d’équilibre explicite à elle seule la distribution spectrale de son rayonnement.
Le spectre de la lumière solaire
Paradoxe : Le Soleil est le corps noir par excellence . Il existe un équilibre intime entre sa matière, de l’hydrogène qui se transforme en hélium au sien de réactions de fusion nucléaires, et l’énergie libérée qui rayonne dans l’espace.
C’est Max Planck qui a eu le premier l’intuition de la formulation de ce qui est appelé aujourd’hui la Loi du corps noir, ou Loi de Planck. Cette relation permet le calcul d’une grandeur M(λ, T) que l’on nomme l’émittance monochromatique du corps noir .
M(λ, T) s’exprime en watts par mètre carré de source d’émission et par mètre de longueur d’onde du rayonnement, donc en Watts par mètres cubes. C’est donc, pour un corps noir en équilibre thermique à la température thermodynamique T, la densité de puissance transportée dans la raie spectrale de longueur d’onde λ .
Son expression mathématique, non justifiée théoriquement par Planck, est la suivante :
 Les valeurs des deux constantes a et b figurant dans l’expression de M(λ,T) sont les suivantes :
Les valeurs des deux constantes a et b figurant dans l’expression de M(λ,T) sont les suivantes :
Remarque importante : C’est la température thermodynamique T = 273 K + θ °C qui est seule pertinente, car la température exprimée en degrés centigrades n’a guère de sens physique . Affirmeriez-vous qu’à une température de 2 °C, vous avez deux fois moins froid qu’à 1 °C ? Par contre, tout le monde sera d’accord pour reconnaître qu’entre 274 K et 275 K, il n’y a guère de différence sensible.
À partir de cette Loi de Planck qui exprime une densité monochromatique, on peut intégrer sur toute l’étendue du spectre de fréquence pour obtenir alors la puissance totale rayonnée par unité de surface (On l’appelle l’émittance totale, en Watts par m2 de surface de la source de rayonnement). C’est la loi de Stefan :
Les courbes tracées sur la figure ci-dessus montrent que la longueur d’onde λm du pic de densité d’énergie se déplace vers les courtes longueurs d’onde lorsque la température T augmente. C’est la Loi de Wien (1864-1928), physicien allemand Prix Nobel de physique 1911 :
C’est l’application de la loi de Stefan qui nous permet d’avancer dans notre compréhension du comportement de l’atmosphère terrestre en calculant l’émittance du Soleil :
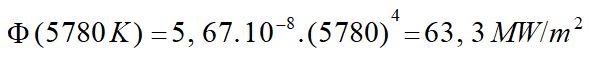 ( 5780 K est une valeur un peu plus précise de la température thermodynamique de la surface du Soleil, sa partie radiative).
( 5780 K est une valeur un peu plus précise de la température thermodynamique de la surface du Soleil, sa partie radiative).
En assimilant le Soleil à une sphère d’un diamètre de 1,4 million de km (R ~ 7.108 m), sa surface d’émission est donc de :
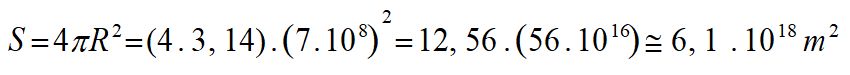 D’où le flux total L du rayonnement solaire dans tout l’espace :
D’où le flux total L du rayonnement solaire dans tout l’espace :
Le faisceau d’énergie solaire intercepté par la Terre a une aire π R2.
L’énergie de ce faisceau se répartit (en 24 h) sur une surface 4 π R2
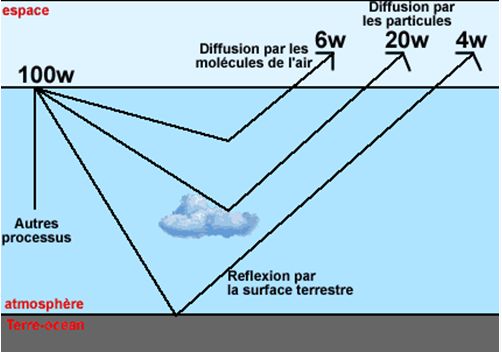
L’énergie solaire moyenne (moyenne sur l’ensemble de la surface de la Terre, et sur l’année) disponible en un point de la Terre, en l’absence d’atmosphère, ou avec une atmosphère parfaitement transparente au rayonnement, est donc seulement égale au quart de 1400 W/m2 soit environ 350 W/m2
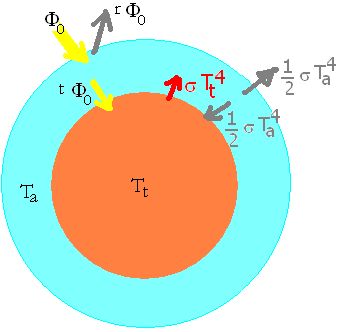
Ta : une température moyenne
r : l’albédo planétaire (c’est ainsi que l’on comptabilise l’énergie renvoyée par réflexion)
a : un coefficient d’absorption du rayonnement solaire
t : un coefficient de transmission du rayonnement solaire, satisfaisant à la condition : r + a + t = 1
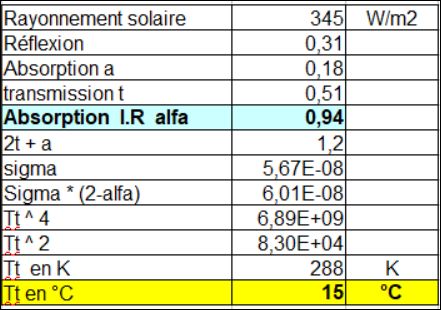
On voit que plus cette absorption d’énergie à basse température par l’atmosphère est faible, plus le dénominateur du quotient ci-dessus va augmenter, entraînant ainsi la diminution de la température d’équilibre de la Terre Tt .
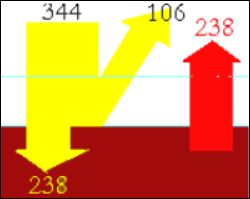
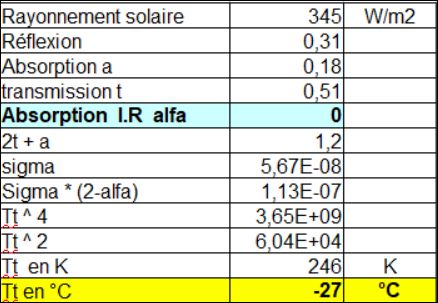
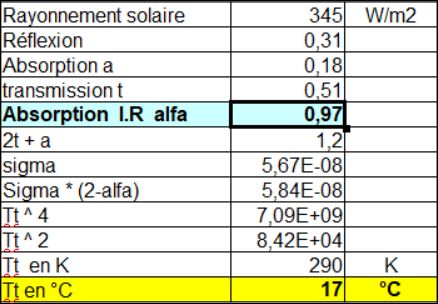
Sans cet effet, c’est-à-dire avec α = 0 , voici ce que l’on obtiendrait :










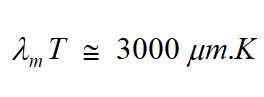








Toujours aussi clair et passionnant, merci Pierre !
Prenez soin de vous,
Olivier