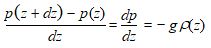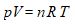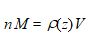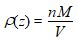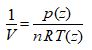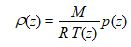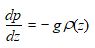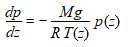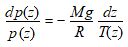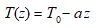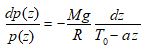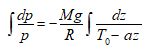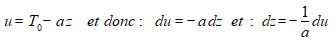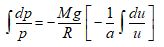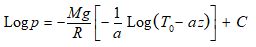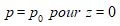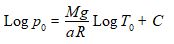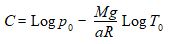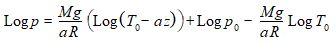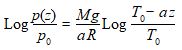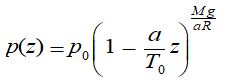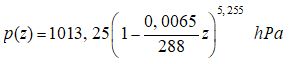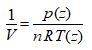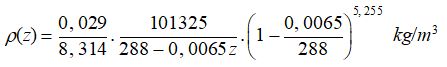Ce billet s’intercalant entre la troisième et la quatrième contribution à la série commencée se veut un rattrapage à un ‘ oubli ‘ de ma part. Celui de traiter le sujet des variations de la masse volumique de l’air sec . Je répare donc aujourd’hui cette lacune .
Pression atmosphérique p(z) , Température T(z) et Masse volumique de l’air sec ρ(z) en fonction de l’altitude z.
La première grande idée en matière de compréhension de la physique appliquée à la météorologie est de commencer par acquérir une connaissance solide des caractéristiques essentielles du domaine concerné, à savoir l’atmosphère terrestre.
C’était l’objet d’un premier billet récemment posté sur ce blog, et qui a l’ambition d’être l’ouvreur d’une série de dix . Un échange privé de commentaires avec l’un des membres du Club de physique de l’Université Tous Ages de Vannes m’a convaincu que l’exposé que j’avais donné de cette première grande idée était trop incomplet. C’est pourquoi, avant de passer à la publication de la quatrième grande idée pour comprendre la météorologie, j’ai compris que je devais aux lecteurs de ce blog les compléments ci-après :
• Tout d’abord, un calcul complet justifiant le modèle d’atmosphère standard de l’OACI, l’Organisation Internationale de l’Aviation Civile .
• Ce premier thème met en évidence la nécessité d’adopter pour se faire un modèle standard de loi de variation T(z) de la température de l’air sec en fonction de l’altitude z.
• Ensuite, un développement compréhensible de la loi de variation de la masse volumique ρ(z) de l’air sec en fonction de l’altitude. En effet, la seule mention de cette relation ρ(z) dans le premier billet était la phrase suivante : « Mais c’est oublier que la température T de l’atmosphère varie avec l’altitude z . Comme l’air est compressible, sa masse volumique est donc une fonction décroissante de la température en fonction de z » .
Voici donc les trois compléments nécessaires :
Nous avons déjà dit que l’idée de l’atmosphère que nous retenons à ce stade de notre exploration de la météorologie est complètement réductrice et simplificatrice. Nous acceptons l’idée d’une atmosphère composée d’un unique gaz qui est de l’air sec. Pas d’humidité dans l’air, nous sommes donc loin des notions de pluie ou de neige. Ce n’est pas fini, nous ignorerons tout mouvement pour demeurer rigoureusement dans le domaine de la statique. Exit donc les vents. Enfin, cet espace statique sera aussi supposé isotherme, c’est-à-dire écarté de tout échange de chaleur.
Dans cette atmosphère pure vue de l’esprit donc, nous noterons :
p(z) , la pression atmosphérique à l’altitude z .
ρ(z) , la masse volumique de l’air sec à l’altitude z .
T(z) , la température de l’air sec à l’altitude z .
g , l’accélération de la pesanteur : g = 9,805 m/s2 .
La variation hydrostatique de pression entre les altitudes z + dz et z est la suivante :
d’où on tire :
Selon la thermodynamique, le comportement d’un tel gaz parfait est régi par la loi suivante, dite des gaz parfaits :
Dans cette loi :
V est le volume occupé par le gaz, en m3 .
n est le nombre de moles de gaz dans le volume V
( la mole est l’unité légale de quantité de matière)
R est la constante des gaz parfaits : R = 8,314 J . mol -1 . K -1 .
T est la température thermodynamique moyenne dans le volume V, en Kelvin
En tenant compte de ce que par définition :
( n moles de masse unitaire M forment la masse totale d’air contenue dans le volume V, soit encore ρ(z) V .)
On peut alors écrire :
et en tirant n/V de la loi des gaz parfaits :
l’expression précédente de ρ(z) prend la forme :
L’équation différentielle :
peut alors s’écrire :
Il n’est pas mauvais de vérifier l’homogénéité de cette équation :
M, on l’a dit est la masse d’une mole, en kg/mol donc.
Le produit Mg s’exprime donc en Newton/mol
Le produit RT représente l’énergie d’une mole, donc des J/mol
On voit alors que le quotient Mg/RT s’exprime en N/J, soit des m–1
On a donc bien de chaque côté du signe = des Pascal par mètre, soit un gradient de pression .
L’équation différentielle à laquelle nous sommes parvenus peut se mettre sous la forme d’une équation à variables séparées :
Malheureusement, si l’intégrale du premier membre est évidente – Log p(z) — le second membre n’est pas intégrable, puisque comportant la fonction inconnue T(z). Force est donc, si on désire parvenir à exprimer une distribution de la pression atmosphérique en fonction de l’altitude, d’adopter une distribution de température T(z) vraisemblable.
II – Température T(z) en fonction de l’altitude
Pour ce faire, la meilleure solution est de recourir à des mesures systématiques de profils de températures le long d’une verticale dans l’atmosphère. C’est ce qui a donné lieu au développement de la technique des radiosondages atmosphériques par ballons sondes. Le boîtier de la radiosonde comprend un ensemble instrumentation afin de mesurer la pression, la température et l’humidité, et un émetteur radio assurant la transmission des données.
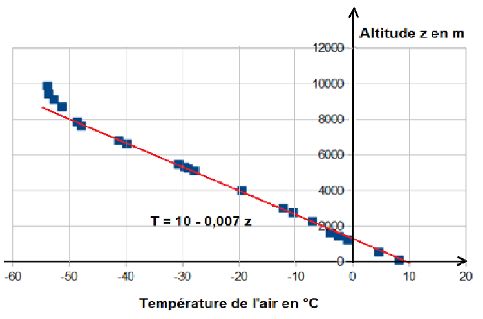
Le diagramme ci-dessous montre le résultat d’un radiosondage effectué à Brest Guipavas le dimanche 29 novembre 2009 à 00 H 00 T.U :
Ce résultat, ainsi qu’un grand nombre d’autres, suggère la pertinence d’une loi linéaire de décroissance de la température au fur et mesure que l’on monte en altitude. Dans ce cas particulier où le sondage a eu lieu à 00 H 00 T.U fin novembre, la température au sol de + 10 °C peut apparaître plutôt élevée, mais nous sommes à Brest .
En pratique, on s’accorde en météorologie pour adopter d’une manière standard un état moyen de l’atmosphère ainsi défini par la loi :
T(z) est la température thermodynamique de l’air sec, en kelvin .
La valeur standard adoptée est : T0 = 288 K ( soit 15 °C) . Nous découvrirons dans un prochain billet la justification de ce choix.
a est le gradient dT/dz , en l’occurrence la pente moyenne des distributions linéaires couramment observées expérimentalement .
La valeur moyenne adoptée est : a = 0,0065
On peut maintenant reporter cette valeur de T(z) dans l’équation différentielle en p(z) précédente :
et obtenir ainsi l’équation facilement intégrable suivante :
et donc :
Pour calculer cette intégrale, on pose :
ce qui conduit à :
et au résultat d’intégration suivant :
et en revenant à z :
La constante d’intégration C est déterminée par la condition initiale :
qui conduit à :
d’où :
En reportant alors C dans l’expression de Log p, il vient :
soit finalement :
expression qui s’intègre pour donner :
expression dans laquelle :
a est en K/m, a/T0 en m -1 et donc [ 1 – (a/T0) z ] un nombre pur.
M est en kg/mol
g en m /s2
R en J. mol -1 . K -1
M g est donc en ( kg . m /s2 ) / mol
a R est en (K/m) . [ ( kg . m /s2 ) . m ] mol -1 . K -1 soit en : ( kg . m /s2 ) / mol comme M g
L’exposant M g/ a R est bien un nombre pur
et la formule donnant p(z) est bien homogène à une pression de chaque côté du signe égal .
Réunissons maintenant les valeurs numériques qui permettront de faire les calculs déterminés par la relation ci-dessus . En fait, nous les avons toutes déjà données lors le leur première apparition précédemment.
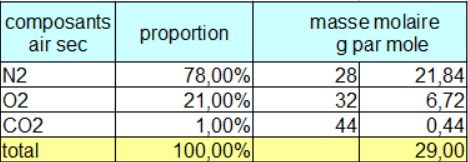
À l’exception de la masse molaire M de l’air sec, que nous allons donc calculer dans le tableau suivant, sachant que l’air sec est composé de 21 % de dioxygène et 78% de diazote, le pourcent restant étant essentiellement du CO2 :
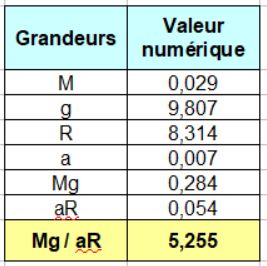
Désormais, nous pouvons récapituler toutes les données numériques nécessaires au calcul de la pression atmosphérique standard OACI :
La relation permettant le calcul de la pression atmosphérique standard OACI prend donc la forme exploitable suivante, en se souvenant de la valeur numérique de p0 déjà vue ( billet initial) : p0 = 1013,25 hPa
Le tableau suivant exécute ce calcul de p(z) pour les altitudes z = 0 jusqu’à z = 20000 m
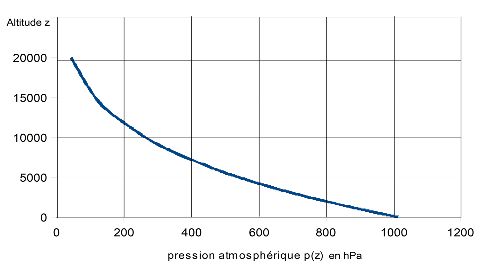
Calculs qui permettent de tracer la courbe p(z) suivante :
III – Masse volumique ρ(z) en fonction de l’altitude
Il ne nous reste donc plus à étudier que la variation de la masse volumique ρ(z) de l’air sec en fonction de l’altitude z . Pour cela, reprenons la loi des gaz parfaits :
Dans cette loi :
V est le volume occupé par le gaz, en m3 .
n est le nombre de moles de gaz dans le volume V
( la mole est l’unité légale de quantité de matière)
R est la constante des gaz parfaits : R = 8,314 J . mol -1 . K -1 .
T est la température thermodynamique moyenne dans le volume V, en Kelvin
Reprenant alors ce que nous avions déjà exposé :
( n moles de masse unitaire M forment la masse totale d’air contenue dans le volume V,
soit encore ρ(z) V .)
on peut alors écrire :
et en tirant n/V de la loi des gaz parfaits :
l’expression précédente de ρ(z) prend la forme :
Il ne reste donc plus qu’à reporter dans cette expression les deux formulations obtenues précédemment :
Les valeurs numériques des différentes grandeurs physiques figurant dans cette expression de ρ(z) ont déjà été précisées plus haut :
M = 0,029 kg . mol –1
R = 8,314 J . mol –1 . K–1
p0 = 101325 Pa
T0 = 288 K
a = 0,0065 K . m –1
g = 9,805 m.s –2
Le calcul des valeurs numériques de ρ(z) se fera donc en appliquant l’expression suivante :
ce que réalise le tableur suivant :
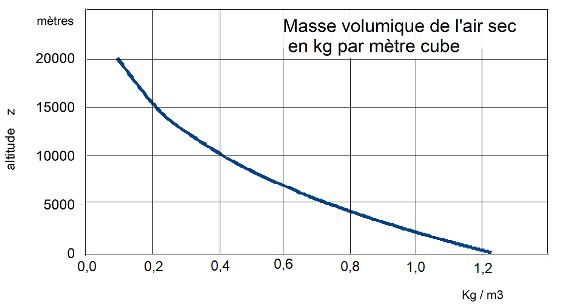
à partir duquel on trace la courbe ρ(z) suivante :
* * * * *