Voici venir la fin de cette série. Vous avez déjà pris connaissance de huit grandes idées :
I – Bien se persuader que la météorologie est avant tout une discipline de physiciens soucieux de comprendre l’évolution dans le temps de deux paramètres fondamentaux : la pression atmosphérique et la température de cette atmosphère ( Billet du 6 avril 2020 complété le 18 avril).
II – Ne pas perdre de vue que faire de la physique, c’est presque toujours étudier des transferts d’énergie. Dans le cas de la météorologie, il s’agit d’analyser la répartition et l’effet du rayonnement thermique reçu du Soleil. ( Billet du 7 avril 2020) .
III – On pourra alors préciser les répartitions des températures moyennes de l’atmosphère et introduire la nécessité de l’existence de l’effet de serre . Ce qui impose l’idée d’une complication accrue de la composition de l’atmosphère ( Billet du 10 avril 2020) .
IV – La nécessité impérieuse de prendre en compte le caractère tridimensionnel, et qui plus est sphérique, de l’atmosphère. Complexité accrue par le mouvement de rotation de la Terre sur elle-même, d’où une force de Coriolis qui, combinée avec les échanges thermiques, génère le phénomène des ondes de Rossby ( Billet du 20 avril 2020).
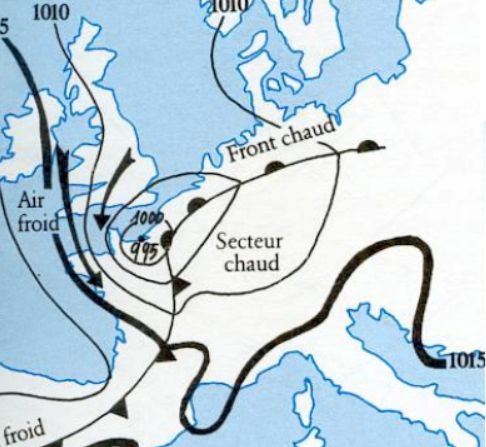
V – Il en résulte alors l’existence d’un front polaire, parcouru régulièrement de systèmes complexes appelés des perturbations, phénomènes majeurs des changements de temps à nos latitudes ( Billet du 23 avril 2020).
VI – Rien en météorologie ne pourra être expliqué et compris sans la prise en compte de la présence d’eau dans l’atmosphère, le plus souvent à l’état de vapeur, mais aussi sous forme liquide en micro-parcelles liquides ou solides. ( Billet du 1er mai 2020).
VII – La prévision de l’état de l’atmosphère dans le futur proche — objectif essentiel de la météorologie — repose avant tout sur l’identification des grandes masses d’air qui se déplacent dans cette atmosphère, en se disputant l’occupation de l’espace. Deux marqueurs rendent possible cette identification des différentes masses d’air et de leur étendue à un moment donné : le géopotentiel Z500 et la Température Potentielle Équivalente Theta E .
VIII – L’étude de l’historique des situations météorologiques observées dans l’hémisphère Nord met en évidence la répétition continue d’un petit nombre de situations faisant intervenir les mêmes grandes masses d’air. Cette typologie comprend six grands types de masses d’air imposant un type de temps bien caractérisé : L’air polaire maritime. L’air arctique. L’air polaire continental. L’air tropical maritime d’hiver. L’air tropical maritime d’été. L’air tropical désertique.
Mais la seule considération du pourquoi et du comment de ces grandes situations décrites à l’échelle dite synoptique ne saurait nous satisfaire, car in fine l’objectif essentiel de la météorologie demeure l’annonce du détail des conditions locales qui seront rencontrées dans un futur très proche de un à dix jours. Et cette description détaillée comporte en particulier celle du déplacement local de ces masses d’air, à une échelle embrassant une zone beaucoup plus restreinte. Ce qui s’appelle dire le vent qu’il fera.
Les équations de la physique vont alors nous permettre d’avoir une bonne connaissance du vent qu’il va faire, et cela sans avoir besoin de mettre des anémomètres partout.
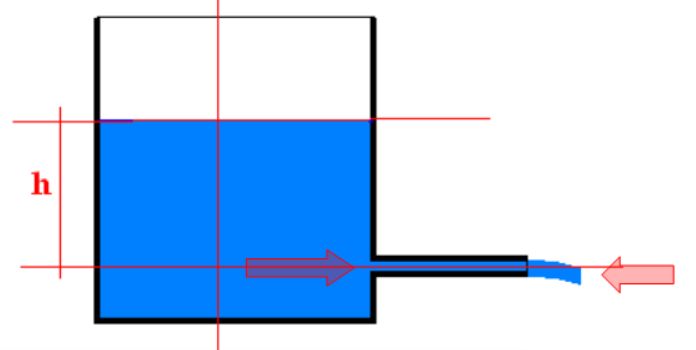
Commençons par regarder une expérience d’hydraulique très simple, celle de la vidange à l’air libre d’un réservoir d’eau :
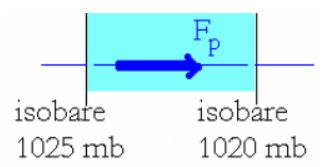
C’est l’excès Δp de pression horizontale à l’entrée du tube, par rapport à la pression atmosphérique régnant à sa sortie, qui provoque l’écoulement du fluide .
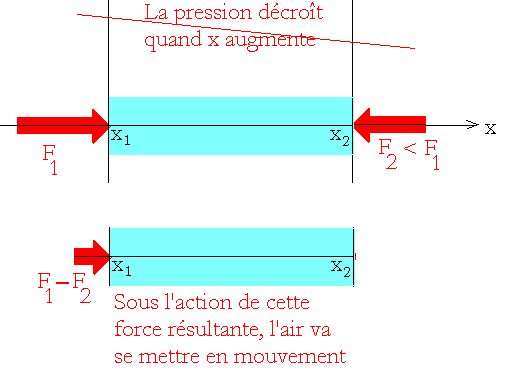
Tous les mouvements au sein de l’atmosphère ont une cause identique . Ce sont les différences de pression dans le sens horizontal qui créent et régissent les vents, en force, et en direction .
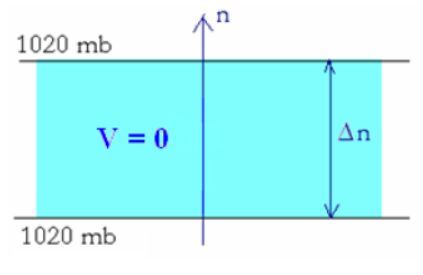
On peut analyser ainsi tous les mouvements au sein de l’atmosphère. Définissons d’abord l’équilibre initial d’un petit volume d’air, petit parallélépipède que l’on regarde vu de dessus dans un plan horizontal . C’est la situation statique suivante :
.
Trop forte, le virage se refermerait ;
Trop faible, il s’ouvrirait.
Nulle, la masse m partirait en ligne droite .
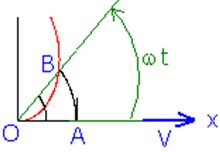
L’accélération horizontale de Coriolis s’exerçant sur tout mobile à la surface de la Terre vaut donc: Ac = 2 ω V sin φ
3
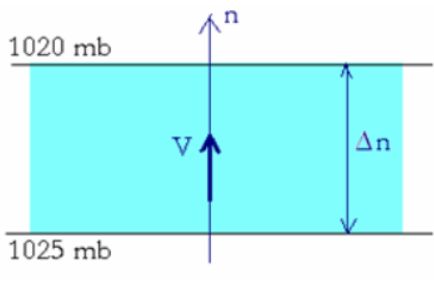
Nous voilà désormais en mesure d’établir l’expression qui va nous permettre le calcul de la vitesse du vent géostrophique dans une situation donnée. La force de pression s’exerçant dans la direction Δn sur une surface S (et appliquée à une masse de fluide ρ S Δn) est égale à :
À la latitude φ, l’accélération de Coriolis est donnée par la relation :
La force de Coriolis a donc pour expression :
De sorte que l‘équilibre géostrophique :
s’écrit :
D’où l’on tire finalement :
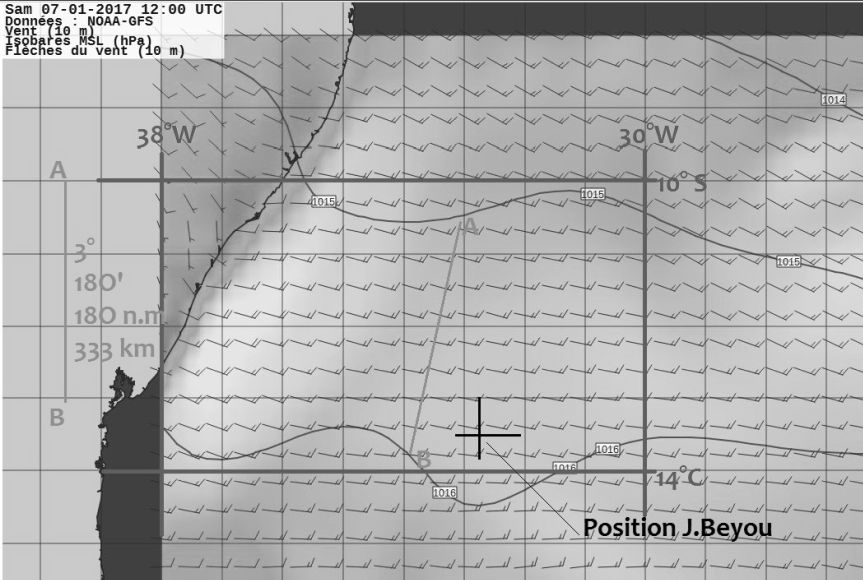
Nous allons tester ce résultat théorique en utilisant les données transmises par le PC course du Vendée Globe. Le samedi 7 janvier 2017 à 12 H 00 UTC, la position de Jérémie Beyou, skipper de ‘Maître Coq’ et 3ème alors de la course, était celle qui est reportée sur la carte ZyGrib ci-dessous :
.
.
Les données nécessaires sont la latitude, deux isobares, et la largeur Δn du tube délimité par ces deux lignes.
Les valeurs numériques nécessaires au calcul du gradient de pression Δp/Δn sont obtenues à l’aide de la carte ZyGrib précédente, dont un extrait agrandi est reproduit ci-dessous :
On y lit que la différence de pression atmosphérique entre les deux points A (sur l’isobare 1015 hPa) et B (sur l’isobare 1016 hPa) est égale à :
tandis que :
On lit sur la carte la latitude φ = 13° 30′ 29 » S
La température de l’air ( à 2 m au dessus de la surface de l’eau est également indiquée dans le fichier ZyGrib : 25,9 °C . On peut alors estimer la masse volumique de cet air :
ρ = 1,17 kg/m3
On a alors toutes les valeurs numériques nécessaires pour appliquer la formule de calcul obtenue plus haut :
Ce calcul est effectué dans la feuille Excel ci-dessous :
résultat à comparer avec les données météo fournies par le fichier ZyGrib , et reproduites ci-dessous :
La concordance entre la force de vent prévue par ZyGrib et le calcul de vent géostrophique est excellente : 15, 1 nœuds dans les deux cas.
Note à propos du logiciel Zygrib :
La version 8.0.1 du logiciel Zygrib, datant de 2016, que j’ai utilisée pour présenter l’exemple de calcul ci-dessus est aujourd’hui obsolète. Il s’est en effet passé de grandes choses depuis cette époque . Zygrib est devenu Xygrib, version 1.2.6, une nouvelle version, toujours OpenSource, c’est-à-dire entièrement gratuite, et toujours plus puissante, car couplée aux logiciels météorologiques les plus récents.
XyGrib est développé et fourni comme un logiciel libre sous licence GNU GPL v3. Il est destiné à être utilisé par toute personne ayant un grand intérêt pour l’analyse météo. En plus des amateurs purs de la météorologie, les navigateurs, les pilotes « privés » et sportifs, les agriculteurs et bien d’autres sont inclus dans cette communauté.
















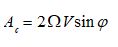
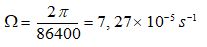
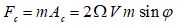
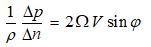
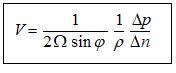

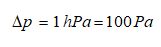
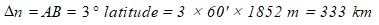


Merci pour cette explication du calcul du vent géostrophique ,c’est toujours avec plaisir que je suis les autres articles de partager pour comprendre
Bien à vous
M Piacentino