Sixième Grande Idée pour comprendre la météorologie

Dans les billets précédents, nous avons déjà mis en avant cinq grandes idées :

I – Interroger la météorologie, dans l’intention banale de savoir ‘ le temps qu’il va faire ? ‘, c’est essentiellement scruter l’atmosphère terrestre pour tenter de prévoir l’évolution dans le temps de deux paramètres fondamentaux : la pression atmosphérique et la température de cette atmosphère ( Billet du 6 avril 2020 complété le 18 avril) .

II – Nous avons identifié le moteur unique gouvernant les grandes évolutions dans l’espace et le temps de l’atmosphère terrestre. Il s’agit du rayonnement thermique dispensé par notre étoile, le Soleil, dont nous avons montré que l’énergie est reçue d’une manière inégale en fonction de la latitude et du moment dans le temps ( Billet du 7 avril 2020) .

III – En mettant en œuvre des connaissances physiques en matière de rayonnement ( notion de corps noir, lois de Planck et de Stefan) nous avons mis en évidence le phénomène d’effet de serre qui permet à l’atmosphère terrestre de connaître une température moyenne au sol de l’ordre de 15 °C actuellement. C’est cette moyenne de 15°C qui risque fortement d’augmenter de 2 °C, peut-être même davantage, si la concentration en gaz à effet de serre (principalement le CO2) continue à augmenter du fait des activités humaines ( Billet du 10 avril 2020) .

IV – Pour comprendre la météorologie, la seule connaissance des flux de chaleur et des températures moyennes qui en résultent que l’on a décrites jusqu’ici est totalement impuissante à nous faire comprendre les mouvements au sein de l’atmosphère. Il nous faut pour cela prendre en compte la sphéricité de la Terre et son mouvement de rotation sur elle-même  . C’est alors que les observations en laboratoire ou dans l’atmosphère elle-même mettent en évidence dans l’hémisphère Nord l’existence de deux grandes zones de l’atmosphère séparées par une frontière nommée front polaire, formant un système d’ondes dites ondes de Rossby, qui se propagent d’Ouest en Est aux latitudes de l’Europe septentrionale ( Billet du 20 avril 2020).

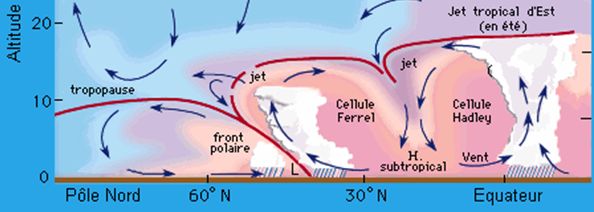
V – L’idée suivante a alors été d’élucider les grandes lignes des mécanismes donnant finalement naissance à ces perturbations qui semblent être l’alpha et l’oméga des présentatrices TV de nos bulletins météo quotidiens avec le refrain que chacun connaît :  » Aujourd’hui une nouvelle perturbation nous arrive par l’Ouest … », avec le plus souvent comme illustration l’unique carte de notre Hexagone. Et nous avons découvert les grandes lignes de ce qui est nommé la frontogénèse, avec ce schéma d’une coupe méridienne ( Billet du 23 avril 2020) :

On y voit que les conditions de formation du front polaire et de son chapelet de perturbations viennent de loin, très loin : très exactement des énormes transferts convectifs pompant l’énergie thermique stockée dans les couches supérieures de l’Océan Atlantique pour injecter dans l’air atmosphérique de la zone intertropicale cette énergie thermique, et cela essentiellement sous la forme de nuages appelés pour cette raison des cumulus. Et ces nuages, puisqu’on les voit, sont faits d’une autre matière que celle des gaz de l’air. Ces cumulus sont des zones de l’atmosphère gorgées d’eau ! D’eau sous forme de microgouttelettes liquides, sinon on ne les verrait pas, mais aussi d’eau qu’on ne peut pas voir, parce qu’elle est là sous forme de vapeur d’eau.

La sixième Grande Idée qui va maintenant être capitale pour comprendre la météorologie sera donc d’abandonner la fiction de l’air sec dont nous nous sommes contentés jusqu’à ce stade de nos exposés, et de nous intéresser à l’air humide, ou plus précisément à l’humidité contenue dans l’air, afin alors d’être en mesure d’expliquer et de prévoir les phénomènes de gelées blanches, de pluie, de grêle, de neige, c’est-à-dire de quelques uns des principaux épisodes météorologiques dont l’existence explique notre intérêt pour cette branche de la physique.

Un beau ciel nuageux avec un grain s’abattant sur la presqu’île de Quiberon

Nous allons commencer par des rappels de physique , et par étudier l’eau dans tous ses états .

D’abord, l’eau à état solide :

Détail du front d’un glacier plongeant dans le Hornsund Fjord, au Spitzberg

Puis, à l’état liquide :

Godafoss, les chutes des Dieux, Nord de l’Islande, vers Akureyri

Enfin, à l’état vapeur :

Un évent de vapeur dans l’environnement géothermal de Námafjall (Islande)

Passons maintenant à un peu de physique (élémentaire) pour que chacun d’entre vous, mes lecteurs, se sente à l’aise quand viendront les développements les plus intéressants. Chacun d’entre vous a mis un jour une bouilloire sur une source de chaleur (cuisinière autrefois ! brûleur à gaz, plaque électrique, feu de camp ?) afin obtenir de l’eau chaude pour le thé ou le café. Mais tous n’ont peut-être pas, ou plus, une conscience claire des phénomènes physiques qui se déroulent dans cette bouilloire schématisée ci-dessous :

Ce phénomène s’appelle un changement de phase de la matière. La matière est ici de l’eau, H2O (des molécules composées chacune de deux atomes d’hydrogène et un atome d’oxygène) et initialement à l’état liquide à la température ambiante, disons 20 °C . On chauffe, ce qui a pour effet d’augmenter la température de l’eau . Il ne se passe rien de notable au début, la température de l’eau augmente, tout simplement., variation qui peut être décrite sur le diagramme (p, T) suivant :

L’état de l’eau au début du chauffage ( pression et température) correspond au point A :  T = 20 °C , p = 1 bar .

La soupape de sécurité de la bouilloire n’étant pas en place, intérieur et extérieur du récipient vont demeurer à la pression atmosphérique ambiante, disons p = 1 bar (la pression atmosphérique ambiante), pendant toute la période de chauffe. L’état du fluide est alors représenté par un point de la droite horizontale A S, point qui se déplace de A vers S . L’arrivée au point S signifie que l’eau vient d’atteindre la température de 100 °C.  Depuis un moment déjà, on pouvait noter des mouvements dans la masse du fluide, puis des bulles se formaient au voisinage des parois, jusque ce qu’a ce que tout le volume liquide soit agité par un nombre croissant de poches de vapeur se dégageant du liquide. L’eau est en train de bouillir. Cette ébullition est un changement profond de l’état de la matière. Les molécules H2O cessent d’être serrées les unes aux autres, s’agitent de plus en plus, leurs mouvements les éloignant de plus en plus les unes des autres, jusqu’à ce qu’elles acquièrent une véritable autonomie. C’est ce qu’on appelle un changement de phase. Le fait majeur est que tant qu’il restera de l’eau liquide, température et pression vont demeurer constantes.

Voici ce qu’on verrait si on pouvait observer une goutte d’eau liquide avec un grossissement de un milliard :

À cette échelle nous distinguerions les molécules d’eau, constituées d’un atome d’oxygène lié à deux atomes d’hydrogène. L’atome d’hydrogène (en blanc) est 16 fois plus léger que l’atome d’oxygène (en noir). La distance O-H est de l’ordre de 1 Angström ( 1 cm = 100 millions d’Angström !) :

Nous verrions ainsi les molécules collées les unes aux autres (elles s’attirent). Nous verrions ces molécules en perpétuelle agitation. Elles oscillent, rebondissent, tournent. L’effet produit est ce que nous appelons la chaleur ou énergie thermique .

Des liaisons peuvent se former entre les molécules d’eau car ce sont des molécules polaires et les charges de signes contraires s’attirent. Ces liaisons, dues à la polarité, s’établissent entre les atomes d’hydrogène de certaines molécules d’eau et les atomes d’oxygène de molécules d’eau voisines. Ce phénomène est nommé « liaisons hydrogène » de l’eau .

Dans l’eau liquide, les molécules d’eau s’associent les unes aux autres sous la forme de paquets de grande taille qui se font et se défont en permanence.

Sans les liaisons hydrogène, la glace devrait fondre vers -100°C et l’eau liquide bouillir vers -65°C.  C’est l’existence de ces liaisons hydrogène qui donne à l’eau ses propriétés physiques exceptionnelles (au voisinage de 0°C, elle se contracte quand on la chauffe et devient plus fluide quand on la comprime), et ses propriétés chimiques non moins exceptionnelles (elle est unique pour dissoudre les sels, acides ou bases en les dissociant en ions positifs et négatifs) .

Quand on chauffe l’eau, l’agitation augmente, ainsi que le volume autour des atomes. Si le chauffage continue, il arrive un moment où l’attraction entre les molécules n’est plus suffisante pour les maintenir ensemble. Elles se séparent les unes des autres et se dispersent en tous sens. C’est l’état de vapeur. C’est ainsi que nous produisons de la vapeur à partir d’eau liquide :

Ces molécules, en heurtant la paroi, exercent une force dF sur chaque cm2 de paroi dS, ce qui est exactement la définition de la notion de pression p :

Cette force de pression  s’exprime en N/m2 ou Pascals (Pa) .

Dans une enceinte de volume V, doublons le nombre n de molécules de vapeur d’eau (ce qui va doubler le rapport n/V), tout en gardant à ces molécules de vapeur d’eau leur même vitesse d’agitation, c’est-à-dire la même température T . Alors, en moyenne, le nombre de collisions avec les parois va doubler, tandis que chaque collision se produit toujours avec la même force d’impact dF :

L’effet produit va être le doublement de l’action globale exercée en chaque point de la paroi de l’enceinte:  la pression p va doubler. Ce résultat constitue la Loi de Mariotte :

À température T constante, la pression d’un gaz ou d’une vapeur est proportionnelle au rapport n/V, n étant le nombre de molécules présentes dans le volume V :

qu’on peut encore écrire :

Le produit pV s’exprime en Joules (C’est une énergie) .

L’énergie de pression d’un gaz ou d’une vapeur ne dépend que de sa température.

Seconde expérience de pensée : Conservons maintenant le même nombre n de molécules de vapeur dans le même volume V. Mais augmentons la température T. Maintenant, les molécules se déplacent plus vite. Elles vont donc frapper les parois plus souvent, et plus fort :

La pression p  =  dF/dS   va augmenter . C’est la Loi de Gay-Lussac  (1787) :

À densité n/V constante (n étant le nombre de molécules présentes dans le volume V), la pression d’un gaz ou d’une vapeur est proportionnelle à sa température T :

Troisième observation :  En 1781, Cavendish avait remarqué que les volumes d’hydrogène et d’oxygène qui se combinent pour former de l’eau sont dans le rapport de 2 à 1 . L’interprétation correcte en fut donnée en 1811 par Amadéo Avogadro, qui émit l’hypothèse que :

Des volumes égaux de gaz, dans des conditions identiques de température et de pression, contiennent toujours des nombres égaux N de molécules :

Cet énoncé constitue la Loi d’Avogadro :

Récapitulons les  3 lois des gaz que nous avons énoncées :

 C’est la Loi des gaz parfaits que nous avions déjà mise à contribution dans les premiers billets de cette série, mais sans lui apporter alors de justification ni théorique, ni expérimentale. Ce manque est maintenant réparé .

Deux précisions à apporter :

a)  Le thème de ce billet est la vapeur d’eau . Nous venons d’expliquer l’origine de la Loi des gaz parfaits . Ne vous inquiétez pas ! Une vapeur ou un gaz désignent le même état de la matière. Seulement, on réserve le nom de gaz aux matières qui ne sont pas présentes à l’état liquide dans les conditions ambiantes de la vie, et de vapeurs aux corps qui dans ces conditions ambiantes ne sont pas liquides (exemples : des vapeurs d’essence, des vapeurs d’alcool, et.)

b) Dans l’énoncé de la loi de Gay-Lussac, figure le mot mole. Je dois vous dire que la définition correcte de cette notion de mole vient d’être modifiée par la Confédération Générale des Poids et Mesures (CGPM) ,et cela depuis seulement novembre 2018 . Voici donc la nouvelle définition légale de la mole :

La mole, symbole mol, est l’unité de quantité de matière du SI. Une mole contient exactement 6,022 140 76 × 10²³ entités élémentaires. Ce nombre, appelé « nombre d’Avogadro », correspond à la valeur numérique fixée de la constante d’Avogadro, NA, lorsqu’elle est exprimée en mol -¹.

La quantité de matière, symbole n, d’un système est une représentation du nombre d’entités élémentaires spécifiées. Une entité élémentaire peut être un atome, une molécule, un ion, un électron, ou toute autre particule ou groupement spécifié de particules.

Cette définition implique la relation exacte NA = 6,022 140 76 × 10²³ mol -¹. En inversant cette relation, on obtient l’expression exacte de la mole en fonction de la constante NA :
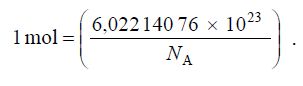Il résulte de cette définition que la mole est la quantité de matière d’un système qui contient 6,022 140 76 × 10²³ entités élémentaires spécifiées.

La loi des gaz parfaits nous permet de préciser la notion que l’on appelle le Volume gazeux molaire dans les conditions normales  de température et de pression, soit :  p0 = 1013 hPa   et   T0 = 273 K 

Pour:  n = 1 mole, sachant que :  R = 8,314 Joule par mole et par K , la loi  pV = n RT  devient dans les conditions dites normales :

Une mole de n’importe quel gaz occupe toujours dans les conditions normales de température et de pression ( 0 °C et 1 atmosphère) le même volume de 22,4 litres.

À ce stade, je vais devoir vous mettre en garde et vous inciter à une grande vigilance et une grande rigueur  dans la manipulation d’expressions littérales telles que celle que je viens d’écrire ci-dessus.  Je m’explique . La dimension physique du terme littéral  RT / p  n’est pas forcément celle d’un volume, comme le résultat  V0 = 0, 0224 m3 l’exige . En fait, tout dépend de la définition adoptée pour la constante R, destinée à rendre compte de la quantité d’énergie, de Joules donc, qu’une certaine quantité de matière peut emmagasiner par degré thermodynamique de température.
Si on compte les quantité de matière en moles, avec donc : R = 8,314 Joule par mole et par K , le résultat du calcul ci-dessus est correct, car l’expression RT / p  a bien les dimensions d’un volume .

Mais si on exprime les quantités de matière en utilisant d’une manière bien plus usuelle la masse exprimée en kilogrammes (kg) , alors la constante R doit s’exprimer en Joules par kilogramme et par degré Kelvin,  et non plus en Joules par mole et par K  comme ci-dessus.

Et cette manière de faire à le grand avantage de mettre en évidence une propriété dimensionnelle qui va nous être fort utile pour la suite de nos réflexions . Faisons donc un peu d’analyse dimensionnelle, ce qui est toujours un point capital en physique théorique .

Les dimensions fondamentales du système d’unités S.I seront notées ainsi :

M pour la masse de la matière
L   pour les longueurs
T   pour le temps
K  pour la température thermodynamique

On écrira alors la dimension d’une accélération : L T-2  et celle d’une force :   M L T-2
La dimension d’une énergie sera donc :  ( M L T-2 ) L  soit : M L2 T-2

La dimension de la constante R sera donc :  ( M L2 T-2 ) ( M-1) ( K-1)  soit : L2 T-2 K-1
et celle du produit RT : L2 T-2

La dimension d’une pression est : ( M L T-2 ) ( L-2 )  soit :  M L-1 T-2

La dimension du quotient RT/p  est donc alors : ( L2 T-2 ) / ( M L-1 T-2  )  soit :  L3 M-1

RT/p doit donc alors s’exprimer en mètres cubes par kilogramme 

Vous voyez bien le trouble potentiel provoqué par la coexistence de deux possibilités pour dénombrer les quantités de matière. On peut le faire de la manière classique en comptant ces quantités en kilogrammes, l’unité légale de masse.  Mais on peut également s’affranchir de la masse ( pourtant une caractéristique exclusive de la matière), et compter en moles . Le quotient RT/p  s’exprime alors en mètres cubes .

Si on adopte la manière classique de compter la quantité de matière en kilogrammes, il faut aussi abandonner l’expression :

R = 8,314 Joule par mole et par K

et la remplacer par des expressions que nous allons découvrir maintenant, et d’abord dans le cas de l’air sec.  On admettra que cet air sec se comporte comme un gaz parfait selon la loi :

Dans les conditions dites normales  (p0 = 1013 hPa   ;   T0 = 273 K), on a vu ci-dessus qu’une mole d’air sec occupe un volume  V = 0,0224 m3 . Nous avons pu calculer, dans un billet précédent, que la masse volumique de l’air sec à 0°C est de 1,276 kg/m3 .

Une mole d’air sec a donc une masse de 0,0286 kg. Et une simple règle de trois nous donne alors :

On peut de même considérer que la vapeur d’eau se comporte comme un gaz parfait, satisfaisant à la loi :

Aux Conditions normales  (p0 = 1013 hPa  ;  T0 = 273 K), une mole H2O ( de masse  0,016 + 0,001 + 0,001 = 0,018 kg) occupe un volume   V = 0,0224 m3 . D’où comme ci-dessus :

En raisonnant ainsi ( les quantités de matière comptées en kilogrammes) on a montré plus haut que le quotient  RT/p s’exprime alors  en mètres cubes par kilogramme . Il en découle que son inverse  p/RT s’exprime en kilogrammes par mètres cubes , ce qui n’est autre que la masse volumique du fluide . Nous venons donc d’établir les deux relations importantes suivantes :

La présence de la vapeur d’eau dans l’air est indissociable de celle de toute nappe d’eau, petite ou grande. Dans l’air au dessus de la surface de l’eau, il y a des molécules d’eau, mais sous forme de vapeur. Ces molécules cohabitent avec les molécules d’azote et d’oxygène qui composent l’air Cette vapeur d’eau devra toujours se trouver en équilibre avec l’eau liquide, comme montré sur la figure suivante :

Tant que la température T (et la pression atmosphérique p) demeurent constantes, le bilan de ces échanges par évaporation et condensation ne peut que demeurer équilibré. Cet équilibre entre les petites quantités de chaleur échangées résulte de ce que :
— un peu de chaleur est absorbée pour évaporer, ce qui tend à abaisser la température T de l’eau ;
—  la même quantité de chaleur est restituée lors de la condensation, ce qui va réchauffer l’eau, et maintenir sa température égale à T .

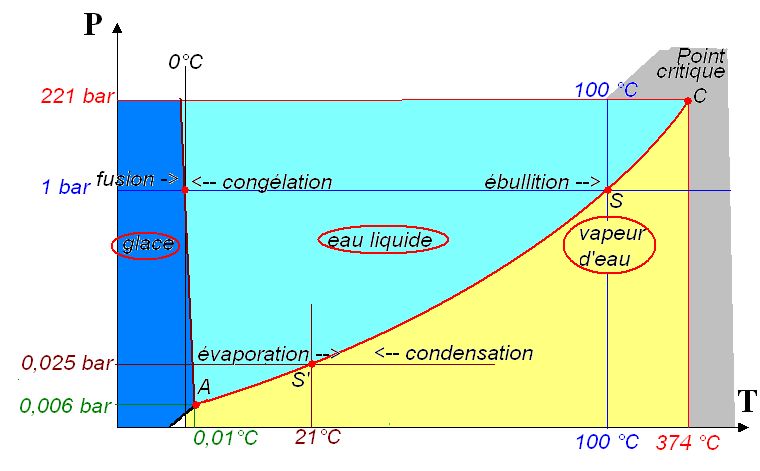
On peut généraliser ces constatations simples pour l’ensemble des états possibles de la matière.  Pour chaque couple de valeurs (pression p, Température T ) il existe trois états possibles de la matière, solide, liquide, gazeux , comme montré sur le diagramme suivant, dédié au cas de l’eau :

Ce diagramme thermodynamique de l’eau montre que le plan (p, T) est divisé en trois zones :
— bleu foncé, pour l’état solide, la glace ;
— bleu clair, pour l’état liquide :
— jaune, pour l’état de vapeur .

Les domaines liquide et vapeur sont séparés par une frontière courbe A S . Chacun des points de cette frontière (qu’on appelle la courbe de saturation de l’eau) correspond à l’un des équilibres décrits plus hauts. Citons trois des points de cette courbe les plus connus :

À la température T = 100 °C , le point S correspond à la pression atmosphérique de 1 bar. C’est l’ébullition totale de l’eau :à la pression atmosphérique normale p = 1 bar , toute l’eau disponible à la surface d’échange sera vaporisée.

À la température T = 21°C , une température ambiante très ordinaire, le point S’ nous montre que l’air sec à la pression atmosphérique sera mélangé à de la vapeur d’eau à une pression partielle de 0,025 bar.

À la température T = 0,01°C , le point A est très particulier. C’est le point triple, auquel, à la pression très faible de 0,006 bar, les trois phases de l’eau (glace, liquide, vapeur ) cohabitent :

Point triple de l’eau en laboratoire

Nous devons mieux comprendre désormais pourquoi notre conception initiale de l’air atmosphérique n’était en fait qu’une mise en route. un point de départ ayant néanmoins l’avantage de susciter en nous maintes questions.

Dorénavant, la compréhension que nous souhaitons acquérir des principaux phénomènes météorologiques passe par la prise en considération d’un air atmosphérique humide que nous allons définir comme le mélange suivant :

La teneur maximale en vapeur d’eau de ce mélange sera bien évidemment limitée par la valeur de la pression de saturation en vapeur d’eau ew  , qui est fonction de la température T , comme le montre la figure ci-dessous :

Pression de vapeur d’eau saturante ew
en fonction de la température

Les coordonnées de cette courbe de saturation sont détaillées dans la table ci-dessous :

(Source : Triplet et Roche, Météorologie générale, École Nationale de la météorologie, 1977)

En météorologie, pour indiquer le degré d’humidité de l’air on utilisera l’une des trois grandeurs suivantes :

— Le rapport de mélange r de l’air humide
— Le rapport de mélange rw de l’air saturé en vapeur d’eau
  — L’Humidité relative U

1 – Le rapport de mélange r de l’air humide 

Il est défini par la relation :

Ce rapport r, qui peut théoriquement devenir strictement nul (air totalement sec), ne peut par contre jamais dépasser (durablement) une limite maximale déterminée par les conditions de saturation (données par la température et la pression atmosphérique) .

Exprimé tel quel, il ne peut pas nous servir à grand chose, car comment accéder pratiquement à la valeur de la masse de vapeur d’eau contenue dans un kilogramme d’air sec ? Cette difficulté est contournée grâce au résultat que nous avons établi plus haut : la masse de vapeur d’eau dans un volume donné V ne dépend que de la pression partielle de vapeur d’eau  e  , qui est elle-même une fonction de la température. On peut donc écrire que :

et en y introduisant les valeurs numériques obtenues plus haut :

2 – Le rapport de mélange rw de l’air saturé en vapeur d’eau :

La situation envisagée est celle du mélange de l’air sec avec de la vapeur d’eau saturante. C’est-à-dire une vapeur d’eau en équilibre avec des gouttelettes d’eau liquide, ou bien des cristaux de glace, en suspension dans l’atmosphère . La taille de ces particules liquides ou solides est généralement de l’ordre 1 à 20 microns, bien trop faible pour qu’elles puissent chuter sous forme de pluie. Mais ce sont elles qui créent les ciels nuageux . Pour ce qui est des précipitations (sous forme de pluie, grêle ou neige), il faudra qu’interviennent des processus de grossissement de ces noyaux initiaux, provoqué par plusieurs mécanismes ( transfert de vapeur d’eau par effet Bergeron, un phénomène d’apparition de gouttelettes sursaturantes par rapport à la glace, à des températures négatives donc, suivie de condensation solide en cristaux qui vont grossir au dépens des gouttelettes . En même temps, phénomènes de coalescence, les éléments les plus gros captant les plus petits au cours de leur chute) .

La forme générale de l’expression obtenue plus haut dans le cas d’une humidité non saturante ( e < ew ) est toujours valable dans la situation de vapeur saturante, en substituant à  e, la pression partielle de vapeur d’eau dans l’air humide non saturé, la valeur de la pression de vapeur d’eau saturante ew :

Cette relation fournit la limite maximale déterminée par les conditions de saturation à  la température T (en °C) et  à la pression atmosphérique p  (en mbar) .

3 – L’humidité relative U :

Enfin, on utilise aussi la notion d’humidité relative, définie par la relation :

dans laquelle :

e  est la pression partielle de la vapeur d’eau dans l’air
ew(T) est la pression de vapeur saturante à T°C

En pratique, U varie de 15% à 100% .

Comment mesure-t-on l’humidité relative de l’air ?

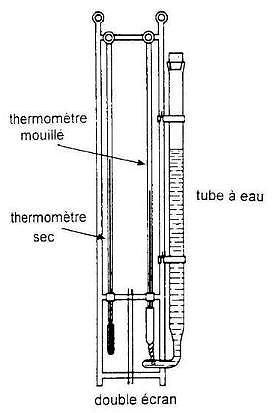
Il existe un instrument, réservé dans la pratique aux météorologistes, qui s’appelle un psychromètre. Cet instrument est constitué essentiellement de deux thermomètres : un thermomètre dit ‘ mouillé ‘ et un thermomètre sec .

Une mousseline entourant le bulbe du thermomètre dit « mouillé » est constamment imbibée d’eau. Cette eau s’évapore plus ou moins vite en fonction de la température de l’air T1 et de l’humidité relative existante U .
Cette évaporation absorbe une quantité de chaleur dont la disparition fait baisser la température du réservoir « mouillé » qui affiche une valeur T2 .
A partir de la baisse de température T1 – T2 observée, on peut alors calculer U .

En pratique, on peut appliquer le tableau à double entrée suivant  :

( Source : http://www.nicole.cortial.net/complements/physique/  )

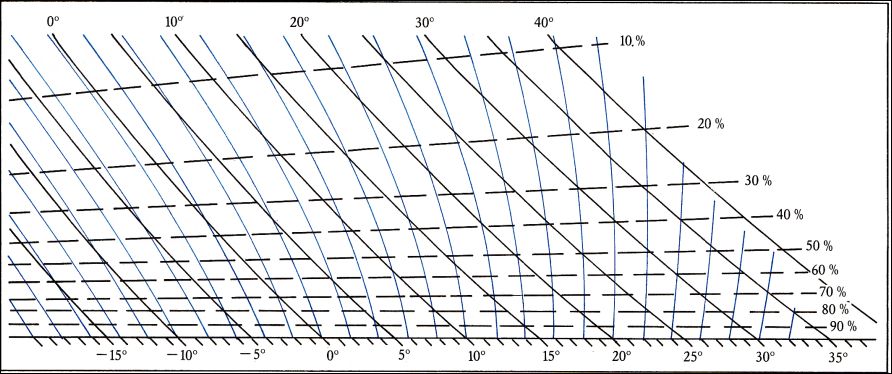
ou bien l’abaque :                                                                                                        

( Source : R.Mayençon, Météorologie marine, Éditions Maritimes et d’Outre-mer, 1982 )

Comment utiliser cette abaque ? Supposons que nous disposions d’un psychromètre et que nous ayons fait les deux lectures de températures suivantes :  Thermomètre sec : 20 °C,   Thermomètre mouillé : 14 °C .  Nous voudrions connaître quelle est l’humidité relative H correspondante.

Deux réseaux de courbes isothermes sont tracées sur l’abaque:

—   un réseau en noir de courbes parallèles descendantes de gauche à droite graduées (en haut) de 0 °C à 40 °C : les températures sèches ;
—   un réseau en bleu-vert en éventail, graduées de -15 °C à 35 °C (en bas) : les températures mouillées .

On a identifié en rouge la température sèche de 20 °, et en bleu la température mouillée de 14 °C . Ces deux tracés se coupent en un point P .
La cote en % de la position de ce point P dans le troisième réseau ce courbes — celles tracées en tirets et pratiquement horizontales — nous donne l’humidité relative cherchée. Ici, et sans avoir besoin d’interpoler :  H = 50 %

Comparons avec le résultat que fournit le tableau donné un peu plus haut :

À l’intersection de la ligne T1 = 20 °C  et de la colonne  T1 – T2 = 6 °C,  on lit  :  H  =  51 % . L’accord entre les deux méthodes est bon .

Pour conclure ce sixième billet de notre série, il est bon de récapituler les idées importantes qui nous ont occupés, et de vous donner quelques lumières sur les sujets que nous aborderons bientôt, dans la continuité de notre projet global . C’est ce que nous allons faire maintenant :

.

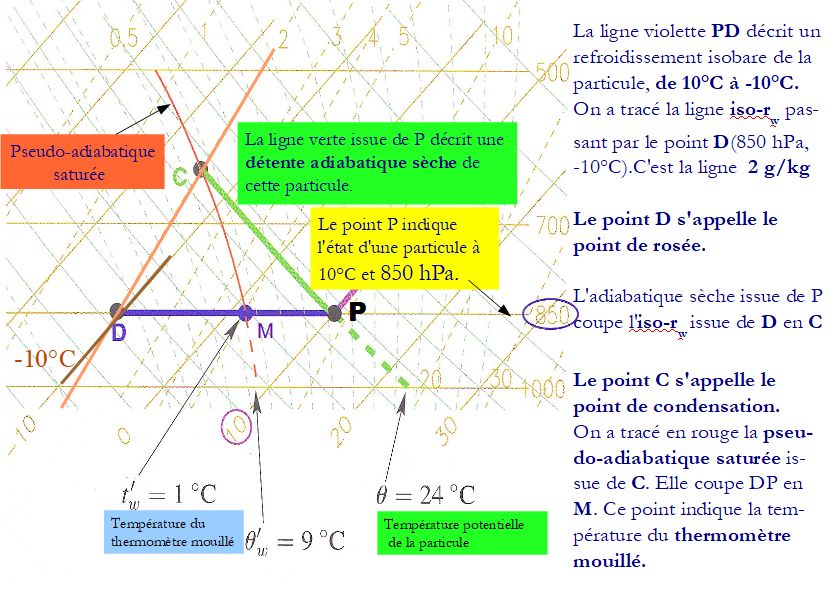
Voici maintenant un premier exemple d’utilisation de l’émagramme 761, afin de vous faire comprendre l’intérêt de chacune de ces cinq familles de lignes iso-valeurs :

Sur ce diagramme se lisent les changements physiques qui peuvent intervenir et modifier ainsi l’état d’une parcelle de l’atmosphère qui pourra passer de P, son état initial ( air humide à la pression 850 hPa et la température de 10 °C.
à C, le point de condensation, par une détente adiabatique sèche .

Un refroidissement isobare aurait pu faire passer la parcelle de P à D , appelé le point de rosée.
Pendant un tel refroidissement à pression constante, la parcelle serait passée par le point M, à la température du thermomètre mouillé .

Un autre outil disponible dans l’arsenal des modèles météorologiques est la simulation des résultats de sondages de l’atmosphère le long de la verticale d’un point déterminé d’un territoire. Nous avions déjà évoqué ces outils en présentant le modèle standard de variation de la température de l’air en fonction de l’altitude.

C’est une telle sortie d’ordinateur qui va nous permettre d’évoquer concrètement comment l’examen des valeurs respectives de grandeurs comme l’altitude, la pression atmosphérique, le point de rosée, l’humidité relative, va concourir à élaborer un diagnostic sur le genre de temps qu’il va faire, si le ciel sera nuageux ou dégagé, s’il va pleuvoir ou non, si le vent va tourner ou forcer, etc.

L’exemple que je prends est celui de l’examen du ciel, vu depuis l’appartement dans lequel je suis confiné pour cause de Covid-19, avec vue plutôt vers le sud, disons du SE au SW. Voici donc ce que je vois :

Vue du ciel vers le SE – SW, à Vannes, le 30 avril 2020 vers 14 H 30

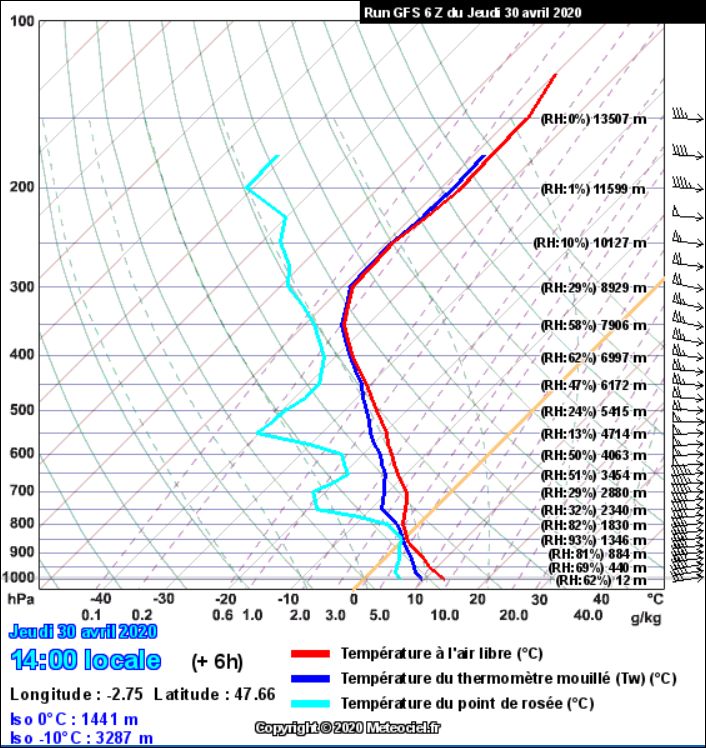
Ces nuages sont des cumulonimbus. À quelle altitude environ sont-ils ? Que me disent-ils ? Je peux trouver une réponse en interrogeant un modèle météorologique librement accessible sur internet, et qui va me tracer les résultats d’une simulation de sondage de l’atmosphère surmontant Vannes, le 30 avril 2020 vers 14 H 00 . Voici ce diagramme :

Ce sondage est très parlant. D’abord il me confirme les trois grandeurs que je peux mesurer moi-même, à l’altitude de quelques 10 à 20 m à laquelle je me trouve : p ≅ 1000 hPa, T ≅ 14 °C, H ≅ 70 %.

Mais il me donne des précisions intéressantes sur mes cumulonimbus . Leur couche est mince (on voit des portions de ciel bleu derrière), et leur localisation en altitude est précise :  vers 1350 -1400 mètres . Vers 1800 m, l’air est déjà beaucoup moins humide.  Juste à la hauteur de l’isobare 0°C, cet air n’est pas assez froid pour subir une condensation isobare susceptible de déclencher une précipitation. Il ne devrait donc pas repleuvoir d’ici ce soir.

Pour en dire plus, il faudrait consulter d’autres sources d’informations également fournies par ce modèle. mais nous n’en sommes pas là. Pas encore.