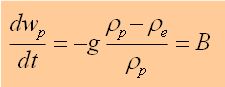Nous voici donc déjà à la fin de cette série de dix billets ayant l’ambition de vous faire découvrir un peu mieux que superficiellement la belle discipline qu’est la météorologie, cette branche de la physique de l’atmosphère dont les bulletins quotidiens sont lus ou regardés par des millions de nos concitoyens, sans que la majorité de ces consommateurs aient la moindre idée de ce qui se cache sous la surface des dits bulletins .
C’est pour le révéler que nous avons ainsi détaillé les neuf idées suivantes :
I – D’abord, avoir une idée claire de ce que sont les deux plus importantes caractéristique physiques de l’atmosphère : la pression atmosphérique et la température de cette atmosphère ( Billet du 6 avril 2020 complété le 18 avril).
II – Ensuite, se dire que faire de la météorologie, c’est presque toujours étudier des transferts d’énergie. En l’espèce, il s’agit d’analyser la répartition et l’effet du rayonnement thermique reçu du Soleil. ( Billet du 7 avril 2020) .
III – On pourra alors préciser les répartitions des températures moyennes de l’atmosphère et introduire la nécessité de l’existence de l’effet de serre . Ce qui impose l’idée d’une complication accrue de la composition de l’atmosphère ( Billet du 10 avril 2020) .
IV – Puis vient la nécessité impérieuse de prendre en compte le caractère tridimensionnel, et qui plus est sphérique, de l’atmosphère. Complexité accrue par le mouvement de rotation de la Terre sur elle-même, d’où une force de Coriolis qui, combinée avec les échanges thermiques, génère le phénomène des ondes de Rossby ( Billet du 20 avril 2020).
V – Il en résulte alors l’existence d’un front polaire, parcouru régulièrement de systèmes complexes appelés des perturbations, phénomènes majeurs des changements de temps à nos latitudes ( Billet du 23 avril 2020).
VI – Mais rien en météorologie ne pourra être expliqué et compris sans la prise en compte de la présence d’eau dans l’atmosphère, le plus souvent à l’état de vapeur, mais aussi sous forme liquide en micro-parcelles liquides ou solides. ( Billet du 1er mai 2020).
VII – La prévision de l’état de l’atmosphère dans le futur proche — objectif essentiel de la météorologie — repose avant tout sur l’identification des grandes masses d’air qui se déplacent dans cette atmosphère, en se disputant l’occupation de l’espace. Deux marqueurs rendent possible cette identification des différentes masses d’air et de leur étendue à un moment donné : le géopotentiel Z500 et la Température Potentielle Équivalente Theta E . ( Billet du 9 mai 2020 ).
VIII – L’étude de l’historique des situations météorologiques observées dans l’hémisphère Nord met en évidence la répétition continue d’un petit nombre de situations faisant intervenir les mêmes grandes masses d’air. Cette typologie comprend six grands types de masses d’air imposant un type de temps bien caractérisé : L’air polaire maritime. L’air arctique. L’air polaire continental. L’air tropical maritime d’hiver. L’air tropical maritime d’été. L’air tropical désertique. ( Billet du 11 mai 2020 ).
IX — Enfin, nous avons découvert une excellente approximation nous permettant le calcul de la force du vent en un lieu donné, à partir des seules données décrivant la champ local de pression atmosphérique autour de ce lieu. C’est la simplification dite du vent géostrophique . ( Billet du 14 mai 2020 ).
La dixième et dernière grande idée que ce billet a pour ambition de vous livrer est que malgré tout, les neuf premiers grands thèmes rappelés ci-dessus ne constituent qu’une introduction, une première trousse à outils pour grands débutants . Il ne faut surtout pas s’en étonner ou s’en désoler, car cette étape de découverte » pour voir » est une nécessité incontournable. Il faut se dire deux choses :
— Bon nombre d’outils encore plus performants, mais plus complexes, restent à découvrir.
— Mais surtout, c’est la pratique assidue et quotidienne de ces outils, et des modes de raisonnement associés, complétée et valorisée par l’observation quotidienne de l’atmosphère, qui peut seule faire de vous un météorologiste amateur averti .
Pour vous donner une idée de ce qui peut être fait de la sorte, je vais reprendre ci-dessous des éléments de présentation que j’avais utilisés dans le cadre du Cours de Météorologie 2014 – 2015 de l’Université Tous Ages de Vannes . L’idée est de vous faire ou refaire découvrir un certain nombre d’outils plus sophistiqués que ceux que nous avons utilisés jusqu’à présent dans les billets précédents.
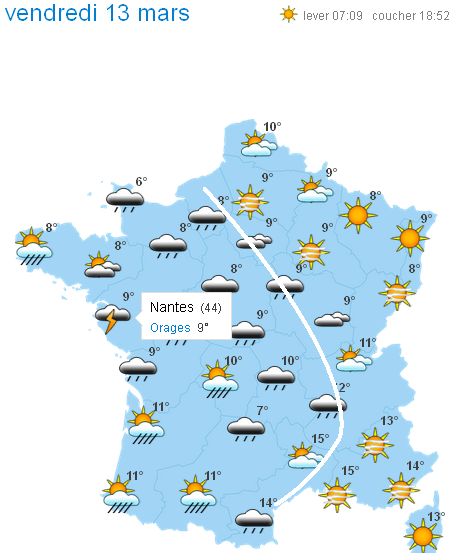
Nous commencerons par regarder la prévision météorologique dont on pouvait prendre connaissance pour le 13 mars 2015, prévision établie par Météo-France il y avait environ 48 heures auparavant, et présentée sous la forme de la carte suivante :
Cette carte annonçait pour une large moitié Ouest de la France un temps nuageux et pluvieux avec quelques éclaircies mais aussi des risques d’orages sur la Loire-Atlantique. Comment la PNT ( Prévision Numérique du Temps )permet-elle d’établir ces prévisions ?
Pour le savoir, nous allons suivre les situations prévues à l’échelle synoptique ( le millier de km ) par le modèle GFS depuis son run daté du mercredi 11 mars 06 H 00 . Voici comment se présentaient alors les différentes masses d’air présentes entre le Groënland et l’Europe de l’Est :
Si vous avez encore en mémoire les six grands types d’atmosphère qu’on a identifiés pour la partie de l’hémisphère Nord qui nous intéresse ( cf. le billet n°8 du 11 mai dernier ), vous devriez reconnaître ci-dessus une invasion d’air tropical maritime, telle que décrite par la figure ci-après :
Vous reconnaissez bien sur chacune des deux cartes ( le schéma général ci-dessus et la situation du 11 mars 2015 plus haut) les grands traits caractéristiques suivants :
–> La vaste zone dépressionnaire sous le Groënland ;
–> Les hautes pressions sur toute la péninsule ibérique ;
–> La longue remontée d’air chaud recouvrant toutes les iles britanniques dans un mouvement courbe typique .
Mais un des outils nouveaux à prendre en compte dont je vous ai annoncé l’importance se trouve mentionné dans le cartouche jaune de la première carte. Pour ce premier d’entre eux, il s’agit de l’examen du jet d’altitude . Ce phénomène est intimement lié à un mécanisme plus fondamental encore pour expliquer le comportement d’ensemble de l’atmosphère dans ce qu’on appelle la zone barocline ( Cette partie de l’hémisphère Nord comprise entre le 40ème et le 60ème degré de latitude Nord et entre le 30° degré Ouest et le 30° degré Est de de longitude). Ce mécanisme est ce qu’on appelle la cyclogénèse . C’est lui qui provoque le défilé des ondes planétaires de Rossby dont nous avons déjà esquissé la formation. Le phénomène se manifeste pleinement lorsque trois facteurs favorables sont réunis :
–> L’existence d’un fort jet en altitude.
–> Un fort gradient horizontal de température.
–> Un fort réservoir d’énergie potentielle utilisable.
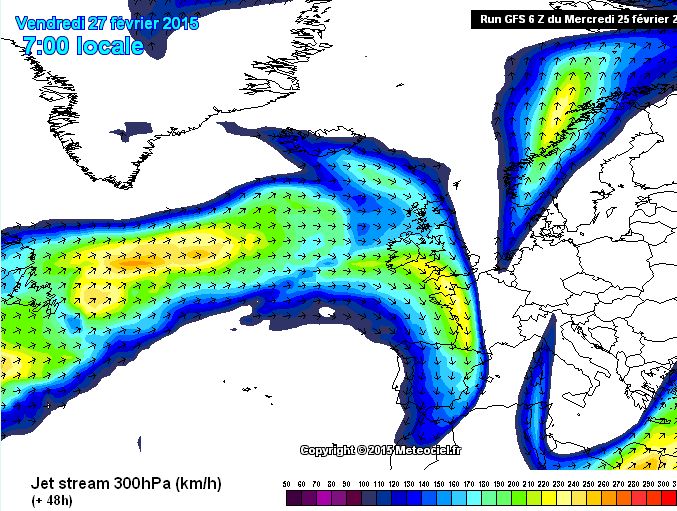
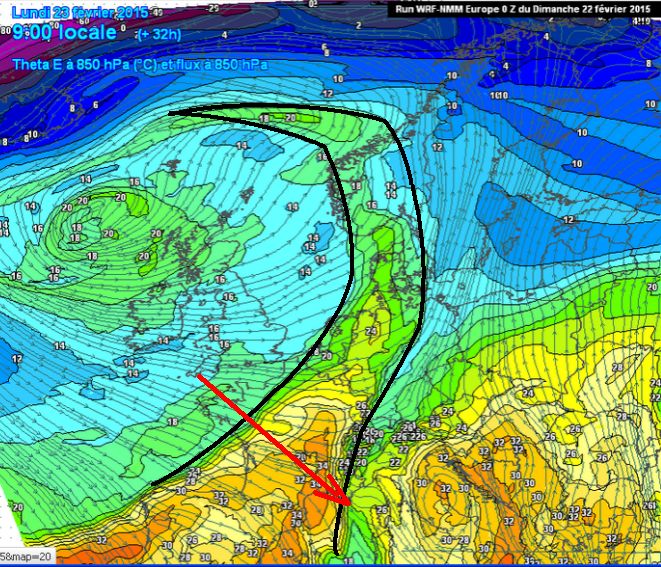
Un exemple de la concomitance de ces trois facteurs nous est donnée le 27 février 2015 à 7 h 00 , avec les trois sorties du modèle GFS ci-dessous :
La carte ci-dessus montre le jet stream à 9000 mètres d’altitude, orienté plein Est à plus de 200 km/h . C’est le premier facteur .
Le second facteur est un fort gradient horizontal de température. Sur la carte ci-dessous, la courbe en noir est l’isotherme -30°C à l’altitude de 5500 m (500 hPa). On constate qu’elle délimite nettement une zone Nord froide (de -30°C à -42°C) , par rapport à une zone Sud chaude (-14°C à -30°C) :
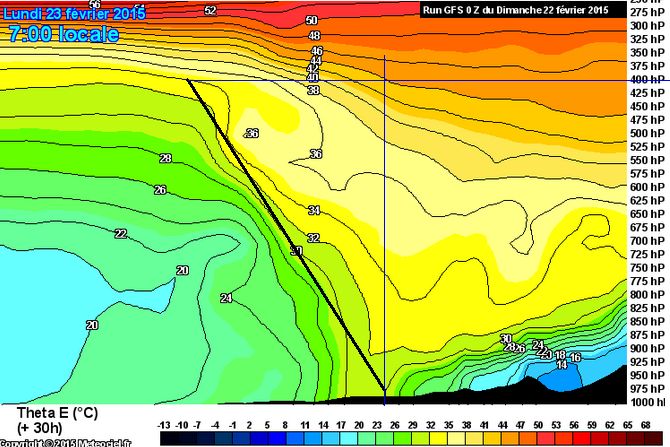
Le troisième facteur favorable est un fort réservoir d’énergie potentielle. La carte ci-dessous, 24 heures avant que la formation de la perturbation ait été vraiment déclenchée, montre des lignes iso-Theta E très serrées, affichant des valeurs très élevées supérieures à 40°C, dans de l’air à -20° -30°C (Attention ! les 40 °C représentent une quantité d’énergie potentielle, qui n’est pas là sous forme de chaleur vive ) :
C’est l’effet combiné de ces trois facteurs qui explique la mise en rotation de l’air dans le plan horizontal . Et c’est cette rotation qui va, en s’amplifiant, créer le centre de la dépression, et un tourbillon vertical :
Dans ce type d’écoulement, les gradients de pression et de densité ne sont pas colinéaires. La force de pression, qui n’est pas volumique, ne dépend pas de la masse de la parcelle d’air. Une même force de pression sera donc à l’origine d’une accélération plus grande sur du fluide léger (à droite) que sur du fluide plus lourd (à gauche). Cette différence d’accélération imprimera en conséquence à la parcelle un couple de rotation en sens inverse des aiguilles d’une montre .
Mais il faut ne pas perdre de vue le caractère global du mouvement tout entier. Rappelez-vous que c’est en tenant compte de l’effet d’entraînement dû à la rotation de la Terre que l’on a mis en évidence les ondes planétaires de Rossby. Pour caractériser des masses d’air en rotation autour du pôle Nord, il faudra donc distinguer :
— La vitesse de rotation d’entraînement :![]() — La vitesse de rotation relative u = Rωr :
— La vitesse de rotation relative u = Rωr :![]() — La vitesse de rotation absolue :
— La vitesse de rotation absolue :
En mécanique des fluides, et donc en météorologie, les équations du mouvement font intervenir le vecteur rotationnel de la vitesse.
C’est en combinant cette grandeur vectorielle et la loi d’évolution de la Température potentielle, que les modèles numériques calculent le produit scalaire suivant, une valeur numérique donc :
C’est ce produit scalaire qui est appelé le Tourbillon potentiel d’Ertel , du nom du météorologiste autrichien Hans Ertel (1904 – 1971).
La formule de définition ci-dessus montre que la valeur numérique de ce paramètre s’exprimera dans le système S.I en :
Cette unité n’a pas reçu de nom. On parlera seulement de pvu, pour potential vorticity unit :
Dans l’ouvrage de référence de Sylvie Malardel, « Fondamentaux de Météorologie, Cépaduès Éditions, 2009 », il est démontré pages 665-66 que cette grandeur P demeure invariante dans toute transformation adiabatique sans changement de phase, ce qui veut dire que :
dP/dt = 0
Comme il est donc conservé au cours du temps, ce Tourbillon potentiel P constitue un traceur des masses d’air.
De surcroît, l’expérience montre que la valeur de ce paramètre reste faible et assez uniforme (0,5 en moyenne) dans toute la troposphère (de 1000 à 300 hPa) de la zone des latitudes de 40°N à 80°N.
La transition entre la troposphère et la stratosphère se fait entre 1,5 et 2 pvu. P augmente ensuite rapidement dans la stratosphère.
C’est pourquoi on définira la tropopause comme la surface 1,5 pvu .
C’est ainsi que, grâce à ce marqueur nouveau (pour vous), le modèle GFS peut mettre nettement en évidence deux zones d’atmosphère caractérisées par des altitudes de tropopause très différenciées : 12000 m pour toute la France et les îles britanniques, 8000 m pour la partie Est de l’Europe :
Le radiosondage effectué à la même heure (01 H locale) le jeudi 26 février par la station de Brest Guipavas confirme parfaitement l’altitude de 12000 m à laquelle le modèle GFS situe la tropopause, au moyen du tourbillon potentiel de valeur 1,5 pvu :
( Note : L’ Université du Wyoming semble ne plus collecter quotidiennement les données de radiosondages en provenance de France, alors qu’elle le fait toujours pour ce qui concerne la Grande-Bretagne, les Pays-Bas, la Suisse, et d’autres … )
La confirmation du résultat du modèle GFS est la même pour le radiosondage effectué au même moment à Münich où la tropopause est localisée à l’altitude de 8150 m (350 hPa) :
L’indice numérique 1,5 PVU que nous venons de découvrir était le premier d’une série d’outils nouveaux (pour nous) qui font toute la puissance des programmes numériques de modélisation de la dynamique de l’atmosphère , décrite dans ses trois dimensions, non plus seulement selon une vue en plan xy , mais aussi selon la verticale z de chaque lieu du plan xy .
La coupe méridienne schématique suivante, vous montre comment la position de la tropopause ( comme montré ci-dessus à l’aide de l’indice 1,5PVU ) permet de localiser la position d’un front ( ici un front froid ) :
Cette coupe méridienne ne doit pas faire oublier qu’une perturbation occupe un volume en 3D. Le front froid représenté en perspective ci-dessous est vu de face par un observateur situé à gauche de la figure, adossé à l’Est, et regardant vers l’Ouest. L’air froid est à droite et l’air chaud à gauche. L’axe y est parallèle au front :
Ce sont seulement grâce aux outils nouveaux que nous venons d’évoquer — analyses en 3D grâce à des coupes planes multiples, à des sondages sur une verticale particulière, au calcul de nouveaux indicateurs — que la prévision numérique du temps ( PNT ) a été rendue possible et performante .
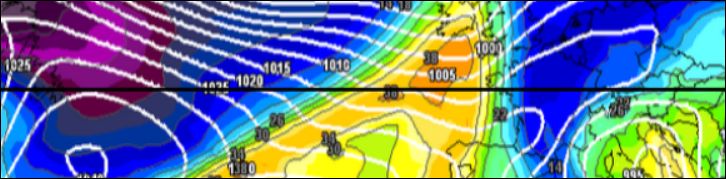
Pour en donner un exemple concret, nous allons reprendre une analyse effectuée en février 2015 . Voici quelle était alors la situation de l’atmosphère le 22 février 2015 à 13 H 00 :
Cette carte classique montrant la distribution de température potentielle équivalente Tetha E à 850 hPa nous montre une dépression assez impressionnante à 956 hPa s’apprêtant à aborder l’Irlande puis la Manche . On y reconnaît le front chaud qui vient d’aborder la Bretagne, et le front froid se déployant jusque dans l’Ouest des Açores. Son centre est à peu près à la latitude de Bergen, soit 60°N .
24 heures après, elle est toujours sensiblement à la latitude de Bergen, soit 60°N :
Nous sommes donc bien dans un schéma zonal . Mais quelle distance cette perturbation a-t-elle parcouru en 24 heures sur cette route plein Est ?
Une caractéristique des perturbations atlantiques importante à connaître est leur vitesse moyenne de déplacement d’Ouest en Est. Pour cela, il faut en connaître deux positions, par exemple à 24 heures d’intervalle, ce qui a été fait avec les deux cartes précédentes :
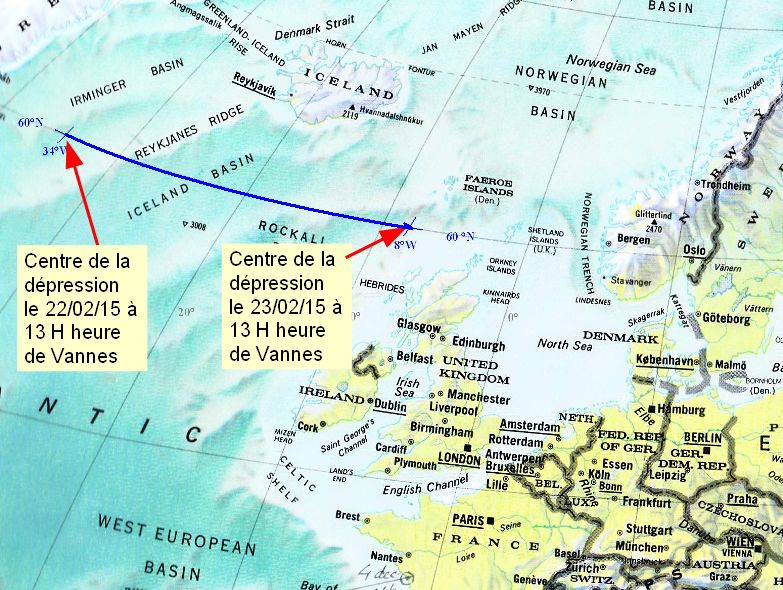
On vient de voir deux cartes GFS montrant toutes les deux la dépression à la même latitude de 60° :
–> Celle du 22 février, 13 H, entre le Groënland et l’Islande, à une longitude estimée à 34°W.
–> Celle du 23 février, 13 H, dans le Nord de l’archipel des Hébrides , à une longitude estimée à 8°W .
La distance parcourue en 24 heures par la perturbation est donc la longueur d’un arc de 26° sur le parallèle de latitude 60°.
Cos 60° = 0,5 .
Le périmètre d’un Grand cercle de la Terre étant de 20000 km, la distance que nous cherchons est donnée simplement par :
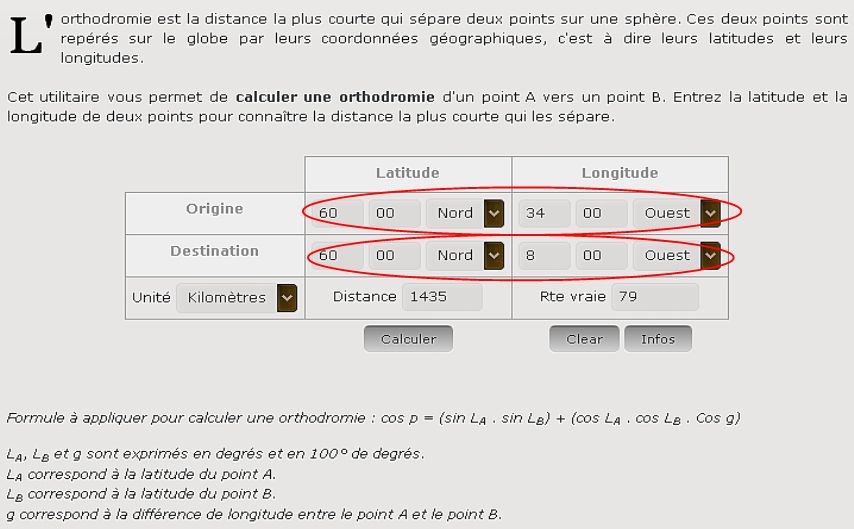
Cette application Java disponible sur le site internet http://aero-training.fr permet de calculer la distance orthodromique entre deux points. Ce qui nous donne la distance parcourue par le centre de la dépression en 24 heures : 1435 km .
On en déduit la vitesse moyenne de progression de la perturbation :
1435 km /24 h ≈ 60 km/h
Pour découvrir plus en détail les caractéristiques d’une perturbation atlantique type telle que celle-ci, nous allons utiliser la capacité des modèles numériques à présenter des coupes verticales dans la partie d’atmosphère représentée :
Ici, à la latitude de Vannes, soit environ 47,6 °W :
Pour remonter un peu plus dans le temps (ici, 4 H heure locale, soit 3 heures avant le lancement du calcul avec les sorties duquel on a effectué les coupes qui vont être montrées ci-dessous , on a utilisé la faculté qu’offre le site Météociel de consulter les archives de GFS.
On voit alors que le front chaud est encore loin sur l’Atlantique :
Et trois heures plus tard :
On peut estimer la vitesse de progression vers l’Est du front chaud en constatant qu’en 3 heures (entre 4 et 7 H heure locale), la Théta E au niveau 700 hPa est passée de 20 à 26°C, soit un gain moyen de chaleur de +2 °C par heure. Sur la coupe, c’est une progression que l’on peut estimer grossièrement à 40 km/h .
La coupe verticale suivante est prévue par le modèle à peu près au moment où l’on a observé dans le ciel de Vannes (vers le SSE) des cirrostratus (voile ténu, couvrant une partie du ciel, d’aspect strié, fibreux ou uniforme) annonçant la pluie quelques heures plus tard :
et la situation à peu près au même moment :
À 13 heures, le front chaud a bien progressé, puisque la Theta E à la longitude de Vannes dépasse maintenant 34°C, soit une augmentation de près de 9°C en 6 heures :
3 heures plus tard, à 16 H donc, la température potentielle équivalente Theta E caractérisant la masse d’air chaud dépasse maintenant maintenant 38°C, à la longitude de Vannes où nous observons sa progression vers l’Est :
Vers 19 h, on peut considérer que la trace du front chaud sur le sol a atteint la longitude de Vannes. Désormais, la Théta E a atteint sa valeur maximale à ce niveau de 700 hPa, et n’augmentera plus :
La trace au sol du front froid à l’arrière de la perturbation fait son apparition à Vannes un peu après lundi matin 4 heures, soit environ 9 heures après le passage de celle du front chaud :
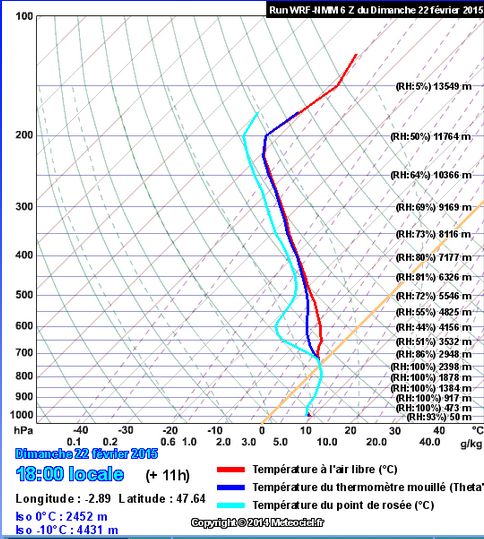
Revenons maintenant en arrière, vers dimanche 22 février, 13 Heures. Pour nous intéresser à la prévision de précipitations , un sujet délicat que nous n’avions encore jamais abordé :
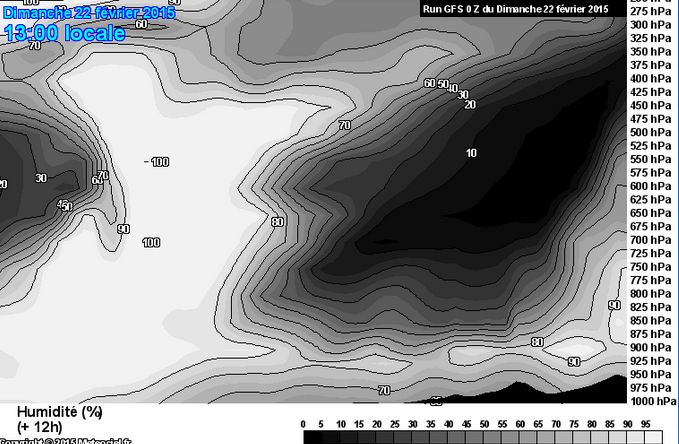
La coupe montrée ci-dessous, cotée en humidité relative nous montre qu’à 13 H il ne peut vraisemblablement pas pleuvoir à Vannes. Les basses couches y sont encore constituées d’air froid et relativement loin de la saturation :
Attention au code de dégradés noir vers blanc adopté par GFS : le noir correspond à un air complètement sec et le blanc à 100 % d’humidité . Cette coupe montre donc qu’à 13 H, l’air saturé d’humidité est encore localisé au proche Atlantique, mais qu’au-dessus de Vannes, l’humidité de l’air ne dépasse pas 70 à 80 % . Il ne pleut donc pas à Vannes à 13 heures .
C’est ce que confirment les cartes de prévisions de précipitations établies par GFS et reproduites ci-dessous :
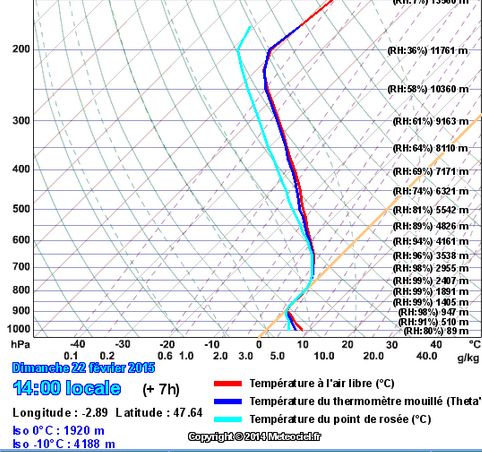
Ces cartes montrent sur le Morbihan un épisode pluvieux débutant un peu après 14 heures et prenant fin vers 22 heures . Il est indispensable de conforter ces prévisions dont la fiabilité est incertaine ( du fait de la difficulté à décrire le phénomène souvent trop localisé pour la résolution des modèles) par l’examen de sondages verticaux de l’atmosphère. De tels sondages sont présentés ci-dessous, pour Vannes :
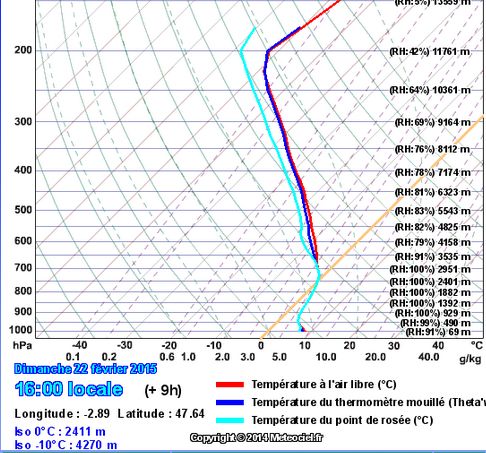
De fait, à 14 heures, il ne pleut pas encore à Vannes . Mais à 16 Heures, ce nouvel émagramme certifie qu’il pleut à Vannes :
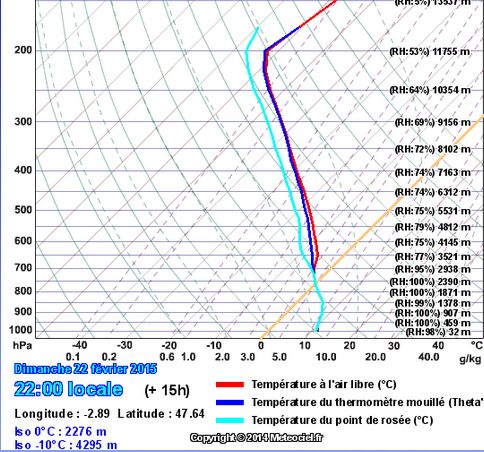
de même encore qu’à 18 h .
Mais un changement s’est opéré, en occurrence un assèchement de l’atmosphère au dessus de 3000 mètres . la fin de l’épisode pluvieux pourrait n’être plus très loin . Mais à 22 H il pleut toujours !
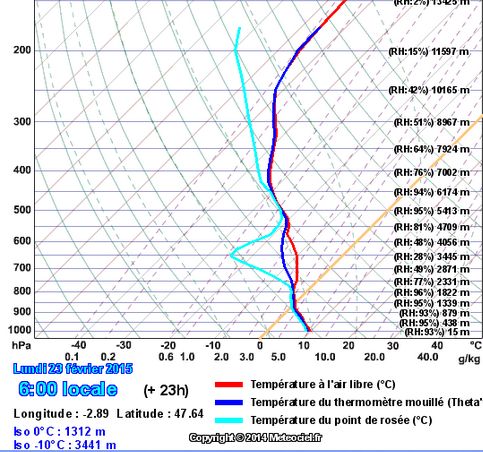
et toujours et encore à 6 heures du matin ! :
L’anomalie de point de rosée vers 3500 m d’altitude que l’on observe sur l’émagramme est évidemment à rapprocher du passage du front froid à la verticale de Vannes, qui vient d’avoir lieu ou qui va avoir lieu :
Normalement maintenant, la suite doit nous montrer que le temps va s’améliorer . Et c’est la carte suivante, sortie du modèle NMM avec une résolution 10 fois plus fine que le modèle GFS précédent (soit 100 fois plus de mailles), qui confirme que le Morbihan en a bien fini avec cette perturbation là, grâce à la remontée d’une belle masse d’air à la Théta E signifiant du beau temps :
ce n’est qu’à 14 heures que cet épisode pluvieux interminable sera enfin terminé, comme l’indique l’émagramme ci-dessous :
Nous avons montré un peu plus haut des cartes de précipitations établies par le modèle GFS . Le paramètre cartographié est une hauteur de pluie prévisible en chaque point du territoire représenté, hauteur exprimée en mm par heure . Comment le modèle parvient-il à déterminer une telle grandeur, en exploitant quels paramètres physiques plus basiques ?
Une réponse très élémentaire, mais essentielle pour vous faire comprendre le principe de cette prévision délicate est la suivante :
En chaque point de l’atmosphère concernée (une zone géographique forcément la plus restreinte possible, et la colonne d’air qui la surmonte), le modèle connaît à chaque instant ( c’est-à-dire à chaque pas de calcul, toutes les 10 minutes par exemple ) les grandeurs physiques suivantes : pression atmosphérique , point de rosée correspondant, température de l’air, humidité relative de l’air .
Ces grandeurs physiques sont connues à chaque instant t dans chacune des mailles de calculs (de petits volumes dx . dy . dz dépendant de la résolution du modèle) . En appliquant alors les équations de la mécanique des fluides et les lois de la thermodynamique, le modèle peut alors calculer les débits de matière ( un mélange d’air sec et de vapeur d’eau) à travers chacune des faces de chaque maille .
Pour ce qui concerne les précipitations, les mouvements de fluide cruciaux sont ceux se produisant selon la verticale, à travers donc les deux faces dx . dy de chaque maille de calcul . Le modèle peut donc, à partir de ces calculs élémentaires, établir des cartes de vitesses verticales .
Attention ! Ces vitesses verticales ne seront pas exprimées en m/s comme en mécanique des fluides classique, mais en hPa par heure. En effet, le paramètre essentiel est bien la pression atmosphérique, qui gouverne à la fois les transferts de masse (ce qu’on appelle le vent ), mais aussi l’humidité relative, et par conséquent les processus de condensation qui conduiront éventuellement à l’apparition de gouttelettes d’eau liquide, et donc à la possibilité de pluie, grêle ou neige , selon les températures .
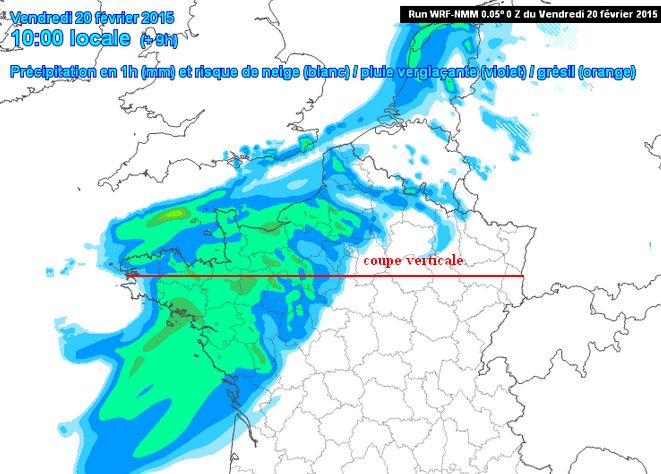
Avant d’aborder la question de l’interprétation de telles cartes, nous allons voir à quoi elles ressemblent, en en examinant une . De nouveau, je puise dans mes documents de la période février – mars 2015 , la sortie suivante :
Sur cette carte indiquant les prévisions de précipitations attendues sur la Bretagne le 20 février 2015 à 10 H 00 ( prévision calculée 9 heures auparavant par le modèle à haute résolution WRF – NMM ), j’ai choisi de demander une coupe verticale de l’atmosphère par un plan contenant le parallèle de Brest . Voici cette coupe dans une édition reportant la distribution de l’humidité relative en fonction de la longitude et de l’altitude :
De la longitude de Brest à celle de Calais, et du sol à 8000 m (350 hPa) l’énorme masse d’air de l’invasion arctique présente une étonnante homogénéité avec une humidité relative de pratiquement 100 %. La partie Est non envahie montre au contraire un air très sec.
La seconde sortie montrée ci-dessous est consacrée à la distribution des vitesses verticales calculée en hPa/heure :
La partie Ouest, déjà presque saturée en humidité, exhibe des vitesses fortement négatives en hPa/h, ces ascendances renforçant l’humidité relative , ce qui est favorable à la formation de précipitations .
Voici un émagramme montrant un sondage à la longitude de Brest, qui montre qu’il pleut à cet endroit :
La partie Est, où l’humidité relative est faible, est le siège de vitesses positives en hPa/h , c’est-à-dire d’une augmentation de la pression atmosphérique, soit une perte d’altitude , ce qu’on appelle une subsidence (par opposition à l’ascendance) . Le résultat en est une diminution de l’humidité relative, une tendance donc à assécher l’atmosphère, caractéristiques d’un temps sec .
C’est bien ce que montre l’émagramme suivant :
Ouf ! Nous venons d’ajouter de nouveaux outils à notre équipement de météorologistes amateurs :
- Le positionnement du jet-stream
- La notion de tourbillon potentiel P, un scalaire compté avec une unité particulière , la pvu ( potential vorticity unit )
- La notion de tropopause, caractérisée par la valeur P = 1,5 pvu
- Le recours aux représentations 3D de l’atmosphères fournies par des coupes verticales et des sondages sur une verticale unique .
- La distribution spatiale des vitesses verticales, comptées en hPa/heure, pour prévoir les précipitations .
Mais ce n’est pas encore tout . Revenons en effet à notre point de départ au début de ce billet : une prévision météo de Météo France pour la journée du 13 mars 2015 :
Cette prévision annonçait des orages sur le pays nantais . Comment peut-on prévoir des orages ? Nous pourrons en avoir une idée, mais avant cela, il nous faut poursuivre dans la voie que nous avons inaugurée plus haut . Il n’est pas possible de se suffire des seules représentations planes fournissant des réseaux d’isobares ( égales pressions atmosphériques au sol ) et d’isohypses ( égales énergies potentielles Z500 ) . Il est nécessaire de scruter le comportement de l’atmosphère dans ses trois dimensions .
Un premier point ( le plus simple ) est de dépasser la première approximation dite du vent géostrophique . Le vent ne souffle pas toujours dans la direction précise indiquée par le tracé des isobares . Voyons en la cause :
Si en altitude, on montre que le vent est sensiblement parallèle aux isobares, ce n’est plus le cas dans les basses couches. Les équations de la mécanique des fluides indiquent alors que le vent « rentre » dans les dépressions, et qu’au contraire, il « sort » des anticyclones :
Sur terre, l’angle du vent avec les isobares est de 30° environ. Sa vitesse est alors égale en moyenne à la moitié de la vitesse géostrophique théorique.
Sur mer, le frottement est moindre, et l’angle du vent avec les isobares n’est plus que de 10° environ . Sa vitesse est alors égale en moyenne aux deux tiers de la vitesse géostrophique théorique.
Les effets tridimensionnels dans la distribution des pressions atmosphériques en centres dépressionnaires ou au contraire anticycloniques conduisent à des différences spectaculaires entre les situations météorologiques qui en découlent :
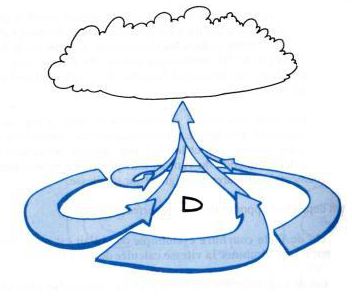
Dans les basses couches sous une dépression, le vent « rentre » dans la dépression. Il y a donc accumulation des particules d’air vers le centre de la dépression. Cette accumulation ne peut se résorber que par un mouvement vertical ascendant.
Ce mouvement entraîne une détente : la pression diminue. La masse d’air qui s’élève voit donc son volume augmenter. Elle fournit ainsi un travail pdV contre son environnement. Comme tout travail, il n’est pas gratuit. Il est prélevé sur la chaleur de l’air, dont la température va diminuer.
De telles ascendances, provoquées par la convergence horizontale accompagnant une dépression, sont la cause du refroidissement de l’air, donc de condensation de l’humidité, et in fine de précipitations.
On pouvait vérifier cet effet en regardant les observations de la situation du 9 mars 2015 à 14 h (heure locale) :
Ce 9 mars 2015, une dépression 975 hPa était centrée dans le NW de l’Irlande, induisant un flux que les isobares de la carte ci-dessus suggèrent comme Sud-Ouest. Mais l’observation de 14 H de la station de Londres -Heathrow signale au contraire un vent « rentrant » de Sud .
L’inverse est observé sous un anticyclone : le vent « sort » de l’anticyclone. Il y a donc dispersion des particules d’air vers l’extérieur. Cet air sortant va devoir être remplacé par un apport venu du haut. Ce qu’on appelle une subsidence.
Ce mouvement descendant provoqué par la divergence horizontale accompagnant l’anticyclone entraîne une compression de l’air et donc un réchauffement. Ce réchauffement va provoquer une évaporation. Les gouttelettes du nuage redeviennent de la vapeur d’eau invisible.
Ce mécanisme explique pourquoi les masses d’air à pression atmosphérique élevée qui constituent les anticyclones sont synonymes de beau temps chaud et sec.
Dans la prévision numérique du temps (NWP), on raisonne sur des briques élémentaires d’atmosphère, à l’intérieur desquelles les grandeurs météorologiques (pression, température, humidité, vitesses) sont moyennées. Cette contrainte exige de conduire une réflexion sur les ordres de grandeurs comparés de :
– la taille de la maille du modèle
– la taille du phénomène atmosphérique que l’on désire prévoir, donc devoir décrire suffisamment finement.
– la taille de la partie d’atmosphère modélisée.
Dans la présentation qui a été donnée de la simplification dite du vent géostrophique, on doit ainsi comparer les ordres de grandeur respectifs des paramètres :
– U, pour la vitesse horizontale du vent (en m/s)
– L, pour l’échelle horizontale du phénomène, une dépression par exemple (en m)
– f , pour le paramètre de Coriolis ( f = 2Ω sinφ ), en s-1.
Si on désigne par u et v les composantes de la vitesse horizontale U du vent, la résultante des forces s’exerçant sur l’air en mouvement et l’accélération de cet air sont proportionnelles. L’évolution du champ de vitesses U(u,v) est donc gouvernée par la grandeur d’un terme de la forme :
Ce terme exprime que la vitesse U du vent en un point P varie au cours du temps car des particules d’air animées de vitesses U différentes arrivent à chaque instant en P. C’est ce qu’on appelle le phénomène d’advection .
La vitesse horizontale du vent U et ses composantes u et v sont du même ordre de grandeur qu’on notera U.
L’échelle des variations horizontales du vent est L
Celle des termes de dérivées horizontales sera donc U/L
L’ordre de grandeur du terme d‘advection horizontale sera donc
U au carré / L
Nous avons vu que la situation géostrophique correspond à l’établissement d’un équilibre entre force de pression et force de Coriolis.
En météorologie, il conviendra donc de comparer l’importance relative de la force de Coriolis et de l’accélération horizontale, afin de se faire une idée de la pertinence de la simplification géostrophique.
On vient de voir que l’ordre de grandeur de l’accélération horizontale est
U au carré / L
On sait par ailleurs que l‘accélération de Coriolis est donnée par 2 Ω V sin φ.
L’ordre de grandeur de la force de Coriolis est donc f U ( avec f = 2 Ω sinφ )
L’estimation du rapport entre le terme d’accélération et le terme de Coriolis est un nombre sans dimension noté R0 que l’on appelle le Nombre de Rossby :
Aux moyennes latitudes, le paramètre de Coriolis vaut :
L’ordre de grandeur de l’échelle synoptique adoptée pour les cartes issues du modèle GFS est :
L’ordre de grandeur des vitesses horizontales de vent est :
Ce qui conduit à un Nombre de Rossby :
Un phénomène météo dont le Nombre de Rossby est sensiblement inférieur à 1 sera essentiellement gouverné par la force de Coriolis. C’est le cas du régime zonal des moyennes latitudes Nord .
Par contre, pour un cyclone tropical, le paramètre de Coriolis ne vaut plus que :
L’ordre de grandeur pour un tel phénomène local n’est plus que :
L’ordre de grandeur des vitesses horizontales de vent est :
Ce qui conduit à un Nombre de Rossby :
Un phénomène météo dont le Nombre de Rossby est sensiblement supérieur à 1 n’aura rien à voir avec la force de Coriolis. C’est le cas des cyclones tropicaux qui peuvent suivre des trajectoires très erratiques.
Reste maintenant le cas des phénomènes convectifs. Il s’agit de phénomènes aux petites échelles, pour lesquels le Nombre de Rossby sera supérieur à 1. Les mouvements de l’air ne sont plus alors contraints par la force de Coriolis. Ils ne sont gouvernés que par la gravité et par la force d’Archimède .
Aux moyennes latitudes, le paramètre de Coriolis vaut :
L’ordre de grandeur de l’échelle aérologique correspondant aux phénomènes convectifs (comme les orages) est typiquement :
L’ordre de grandeur des vitesses horizontales de vent y reste :
Ce qui conduit à un Nombre de Rossby :
En météorologie, on appelle convection l’ensemble des processus qui se mettent en place lorsque l’air est instable du point de vue de la flottabilité. Pour aborder cette notion de flottabilité dans l’atmosphère, il est commode d’imaginer une particule d’air sec, considérée comme isolée dans son environnement supposé au repos, seule la particule pouvant se déplacer.
On suppose aussi que la pression interne de la particule s’adapte instantanément à celle que l’environnement exerce sur elle.
On suppose encore qu’à l’échelle de temps où nous nous plaçons, la particule n’échange pas de chaleur avec l’extérieur ( évolution adiabatique ).
Cette particule n’est en définitive soumise qu’à deux forces extérieures :
– la pesanteur d’accélération verticale -g
– la pression pe exercée par l’environnement
( La résultante des forces de pression extérieures constituant ce qu’on appelle la poussée d’Archimède )
L’équation du mouvement vertical qui résultera pour la particule de l’action de ces deux forces est obtenue en projetant sur la verticale la loi de Newton. Les grandeurs suivantes vont intervenir dans cette équation :
wp : la vitesse verticale de la particule
ρp : sa masse volumique
pp : sa pression
ρe : la masse volumique de l’air extérieur
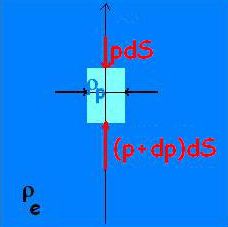
La particule est modélisée par un petit cylindre d’axe vertical selon Oz, de base dS et de hauteur dz.
Son volume est donc dS dz et sa masse ρp dS dz :
La projection sur l’axe vertical Oz des forces extérieures appliquées à cette particule est donc :
soit après réduction des termes :![]()
La symétrie du modèle implique la nullité de la résultante des projections horizontales.
À la résultante verticale Fz des forces extérieures appliquées à la particule, s’oppose la force d’inertie m γz selon l’équation :
En reportant dans cette relation la loi hydrostatique de décroissance de la pression extérieure en fonction de l’altitude :
Il vient :
relation que l’on mettra sous la forme finale :
dans laquelle B est l’expression de la force de flottabilité dans ce modèle simple de la particule aréologique. ( B pour Buoyancy chez les anglo-saxons )
En tenant compte de la loi des gaz parfaits p = ρ R T , la relation ci-dessus prend aussi la forme :
On démontre ainsi les résultats intuitifs suivants :
La particule va être accélérée vers le haut si elle est plus légère ou plus chaude que son environnement, et vers la bas si elle est plus lourde ou plus froide que son environnement .
Nous venons de voir le mécanisme simplifié (on n’a envisagé que de l’air sec) de l’instabilité de flottabilité à l’origine des mouvements verticaux de convection, qui sont une réponse aux déséquilibres énergétiques verticaux provoqués par les grands mouvements de masses d’air.
Il ne faudra jamais oublier cependant que dans l’atmosphère, les processus convectifs sont fortement dépendants des changements de phase de l‘eau. C’est donc la convection humide et précipitante qui nous intéresse en météorologie, ce qui nécessitera une analyse plus fine des processus.
C’est seulement alors que l’on peut envisager le cas des processus convectifs qui s’étendent sur toute la hauteur de la troposphère, processus qui sont à l’origine des orages . Ces phénomènes météorologiques extrêmes dont la figure ci-dessous illustre quelques formes possibles :
( Source : Sylvie Malardel, Fondamentaux de Météorologie, 2009, page 486 )
Cette figure nous explique qu’on peut observer trois grands types d’orages :
(a) IC pour Intra Clouds, avec éclairs intranuages .
(b) CG- pour Clouds-Ground – , nuages – sol négatif .
(c) CG+ pour Clouds-Ground + , nuages – sol positif .
Les nuages qui forment ces systèmes orageux sont des cumulus, dont la formation puis le développement parfois immense sont le résultat des instabilités de flottabilité et des mouvements verticaux de convection décrits plus haut .
Pour comprendre comment l’état de l’atmosphère peut faire passer en quelques heures d’un ciel pur sans la moindre trace de nuage, à un ciel menaçant , obscurci d’immenses masses nuageuses remplies d’éclairs et de grondements, on a inventé une représentation graphique appelée un émagramme .
En France, le diagramme thermodynamique utilisé s’appelle l’émagramme 761. Il permet de représenter à un endroit donné de l’atmosphère et à un instant donné, l’état d’une parcelle d’air décrit par les valeurs des paramètres suivants :
–> La pression atmosphérique ou l’altitude, en hPa.
–> La température, en °C
–> L‘humidité relative, exprimée par le rapport entre la masse de vapeur d’eau et la masse d’air sec contenues dans la particule, en g/kg. On parle alors de rapport de mélange.
L’émagramme 761 apparaît sous le forme d’un graphique compliqué, sur lequel il est essentiel d’identifier cinq réseaux de lignes différentes.
Les deux premiers réseaux de lignes parmi ces cinq, sont les isobares et les isothermes :
Les deux réseaux de lignes suivants, parmi ces cinq, sont les adiabatiques (sèches ou humides) et les pseudo-adiabatiques saturées :
Les pseudo-adiabatiques saturées sont moins inclinées que les adiabatiques sèches ou seulement humides . C’est l’effet de la libération de chaleur due à la condensation qui atténue le refroidissement provoqué par la détente .
Enfin, le cinquième réseau de lignes, représenté en lignes bistres tiretées (ici, continues), donne pour chaque couple (p, T) la valeur du rapport de mélange saturant rw(p, T) :
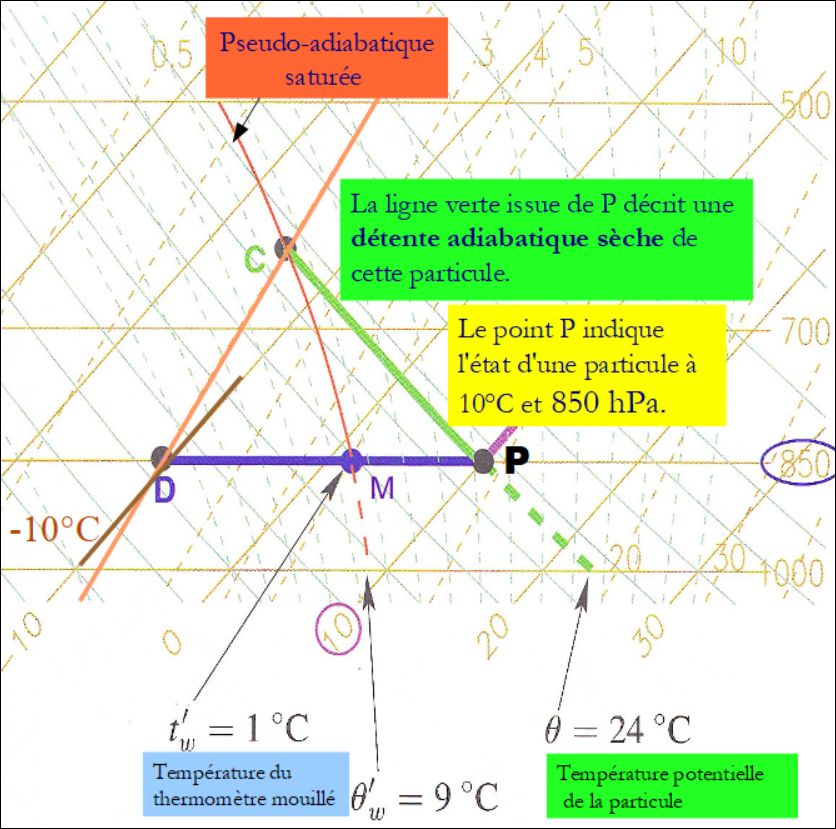
Voici alors, à l’aide de cet émagramme qui a vraiment tout d’un couteau suisse, comment on peut s’y reconnaître dans toutes les évolutions thermodynamiques possibles d’une parcelle d’air humide :
La ligne violette PD décrit un refroidissement isobare de la parcelle, de 10°C à -10°C.
On a tracé la ligne iso-rw passant par le point D(850 hPa, -10°C). C’est la ligne 2 g/kg . Le point D s’appelle le point de rosée .
L’adiabatique sèche issue de P coupe l’iso-rw issue de D au point C . Ce point C s’appelle le point de condensation .
Enfin, on a tracé en rouge la pseudo-adiabatique saturée issue de C. Elle coupe DP en M . Ce point M indique la température du thermomètre mouillé.
Ce sont ces réseaux de lignes iso-valeurs des différentes grandeurs thermodynamiques qui vont nous permettre de nous y retrouver dans les diverses évolutions possibles d’une parcelle d’air, et de comprendre comment il peut y avoir stabilité ou bien au contraire instabilité :
C’est ainsi qu’on pourra suivre la naissance d’un cumulus . Lorsqu’une partie de l’atmosphère est réchauffée par l’échauffement du sol, un mouvement de convection s’établit, provoquant une colonne d’air ascendant qui se constitue ainsi au cœur du nuage naissant, avec des mouvements d’air descendant à la périphérie. En s’élevant, l’air subit une détente adiabatique, ce qui refroidit la vapeur d’eau et provoque sa condensation. Au fur et à mesure que le nuage se charge en eau, le cumulus s’étire en hauteur et forme une tour appelée convectus.
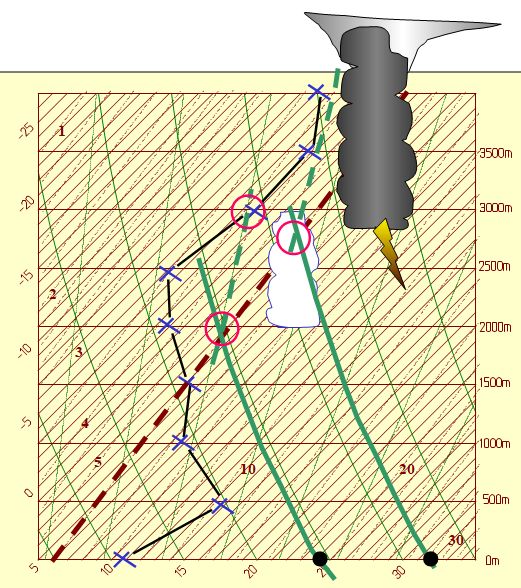
Ci-dessous, le schéma simplifié d’un émagramme résume tout le processus de formation d’un cumulus :
La suite de segments de droites en noir est la courbe d’état de l’atmosphère tôt en début de journée . La température au sol ( altitude arbitraire de 0 m ) est de 11 °C. Cette température du sol va augmenter rapidement dans la journée et sera de 23 °C à 15 heures ( point A) .
À cette altitude de 0 m, et donc à la pression atmosphérique de 1013 hPa, il faudrait un refroidissement jusqu’à la température de 6 °C pour atteindre le point de rosée D , état de saturation en vapeur d’eau de l’air, et donc d »équilibre entre les phases gazeuse et liquide composant le mélange .
Par ce point D, passe une des courbes du réseau d’égal rapport de mélange saturant rw(p, T) .
Cette courbe de saturation est tracée en pointillés rouges sur le diagramme .
Revenons au point A sur le diagramme . La parcelle d’air à la température Tp = 23 °C est plus chaude que l’air qui la surmonte . Elle est donc soumise à une force de flottabilité B positive, proportionnelle à l’écart Tp – Te ( voir l’établissement de ces expressions plus haut) . La parcelle va donc s’élever en altitude, le point représentatif de son état parcourant un chemin tracé en vert continu sur le diagramme. Ce parcours marque un épisode de détente adiabatique . Ce qui veut dire un refroidissement de la parcelle . Cette diminution de la pression et de la température de la parcelle d’air va dure tant que la force de flottabilité positive B proportionnelle à Tp – Te agira .
Ce processus s’achève lorsque le point représentatif sur le chemin vert vient couper la courbe de saturation en pointillés rouges ( point C ) .
L’air de la parcelle est alors à la température de saturation Tp = 6 °C sur le diagramme), ce qui veut dire qu’apparaissent des gouttelettes d’eau liquide dans l’air environnant ( Le diagramme nous dit que cela se passe à l’altitude de 1500 m ) . Cette altitude sera celle de la base du cumulus qui va se former ( Ce nuage n’est rien d’autre que l’accumulation de toutes les gouttelettes d’eau qui vont apparaitre dans cette partie saturée de l’atmosphère ).
Mais le processus de formation n’est pas terminé ! Il vient juste de commencer, et l’air saturé à 6°C de la parcelle que nous suivons est encore plus chaud que l’air qui l’environne, lequel n’est qu’à 3 °C ( regardez le diagramme) . L’air saturé va donc continuer son ascension, résultat de l’écart Tp – Te rémanent, mais cette fois selon le processus traduit sur le diagramme par le réseau de courbes pseudo-adiabatiques saturées ( Le tracé en pointillés verts . C’est une transformation dite pseudo-adiabatique, car elle tient compte de l’apport de chaleur latente libérée par la condensation ). Le cumulus se développe donc et le convectus grandit en hauteur.
Cependant, le moteur B ralentit au fur et à mesure que l’écart Tp – Te diminue . Et de fait, cet écart va s’annuler au point S du diagramme, intersection de la pseudo-adiabatique saturée verte pointillée donnant Tp et de la courbe d’état noire donnant Te . Le diagramme nous dit que l’on est alors à l’altitude de 3300 m . Ce sera le sommet du cumulus .
Et s’il fait encore plus chaud en fin d’après-midi ? L’émagramme schématique ci-dessous suggère une réponse possible, et même probable :
Avec des températures croissantes au sol, le mécanisme que l’on vient de détailler conduit à des cumulus sans cesse plus élevés et plus énormes, et il arrive un moment auquel le processus ne peut plus s’arrêter . Seule la tropopause — le sommet de l’atmosphère donc — sera l’ultime barrière stoppant le développement en hauteur du cumulus dont le sommet s’étalera alors selon la forme d’une enclume, avec déclenchement d’orage assuré .
C’est un épisode orageux de cette nature qu’annonçait le bulletin météo présenté au début de ce billet pour la soirée du 13 mars 2015 , et que revoici de nouveau :
Nous conclurons ce dixième et dernier billet de la série » Dix grandes idées pour comprendre la Météorologie » en vous présentant les grandes lignes des méthodes appliquées par les modèles numériques afin d’en arriver à ce type de prédiction .
Regardons encore une fois le type d’émagramme déjà présenté :
Ce diagramme montre que si une parcelle d’air, initialement dans une situation définie par sa pression p et sa température T, était soulevée adiabatiquement, elle pourrait parvenir éventuellement jusqu’à son point de condensation C ( noté en rouge sur la figure ) .
À partir de ce moment, grâce à la libération de chaleur latente, elle pourrait alors devenir plus chaude que son environnement, et donc continuer son ascension. Mais le plus souvent, ce ne sera pas le cas .
En effet, si la courbe d’état (en noir) donnant la variation de température T de l’environnement de la particule se trouve à droite du chemin adiabatique (en rouge) suivi par la particule, celle-ci, plus froide, ne peut pas monter.
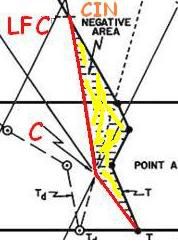
L’intersection de l’adiabatique saturée (en rouge) que suivrait la particule, avec la courbe d’état, est notée LFC. C’est le niveau de convection libre, à partir duquel la température de la particule, ayant rattrapé puis dépassé la température T de l’environnement, peut librement accélérer vers le haut.
Ce niveau de convection libre LFC ne pourra être atteint que grâce à un forçage extérieur ( existence de vitesses verticales dont l’origine est un processus de plus grande échelle, ou passage d’un relief ). Le rôle de ce forçage est de s’opposer au travail de la force de flottabilité qui est une force de rappel vers la position initiale, dans toute la couche sous le LFC.
L’énergie nécessaire est nommée la CIN ( Convective inhibition ) . Elle est proportionnelle à l’aire coloriée en jaune comprise entre l’adiabatique saturée (en rouge) et la courbe d’état de l’air extérieur (en noir) qui se trouve à sa droite, et donc du côté plus chaud .
S’il n’existe pas de CIN, ou si elle a été annihilée par un forçage extérieur, la particule ayant alors atteint le Niveau de convection libre LFB, et donc acquis une accélération positive, va continuer de suivre l’adiabatique saturée jusqu’à ce que celle-ci recoupe la courbe d’état. C’est là le Niveau de flottabilité neutre LNB. Ce sera aussi le sommet des cumulus qui se seront développés.
Le travail positif mis en œuvre par la force de flottabilité B pendant cette ascension du niveau LFC jusqu’au niveau supérieur LNB est appelé la CAPE ( pour Convective Available Potential Energy ) :
Sa valeur est proportionnelle à l’aire coloriée en rouge comprise entre l’adiabatique saturée (en rouge) et la courbe d’état de l’air extérieur (en noir) qui se trouve cette fois à sa gauche, et donc du côté plus froid .
Le point de départ de toute estimation du potentiel convectif de l’atmosphère en un lieu donné est de calculer la vitesse verticale maximale wp que atteindre une particule d’air du fait de l’accélération induite par la flottabilité B . Nous avons établi précédemment la relation :
En multipliant chaque membre de cette relation par wp , on obtient :
C’est-à-dire encore :
qui est une équation différentielle conduisant à l’énergie cinétique verticale de la particule.
S’il y a instabilité , c’est qu’on a :
Et donc la flottabilité B est positive comme la vitesse verticale. Dans ce cas, l’énergie cinétique de la particule augmente, alors que l’énergie disponible pour l’instabilité de flottabilité diminue.
Cette conversion d’énergie est à l’origine du brassage vertical effectué par la convection , ce qui résorbe les accumulations d’énergie dans les basses couches de l’atmosphère .
On obtiendra ainsi une estimation de l’énergie cinétique maximale que peut obtenir la particule, en supposant que cette conversion est totale. Pour cela, on fera la somme des gains en énergie cinétique de la particule tout le long de son ascension entre les niveaux LFC et LNB . Le modèle numérique calculera donc l’intégrale définie :
C’est ce calcul qui fournit la valeur numérique de la CAPE, qui est , on l’a dit, le travail positif mis en œuvre par la force de flottabilité B pendant cette ascension du niveau LFC jusqu’au niveau supérieur LNB . La CAPE est exprimée en Joules / kilogramme .
Un autre index simple , mais d’une importance capitale, est également calculé par chaque modèle . C’est l’indice L I ( pour Lift Index) .
Sa définition est très simple : C’est la différence entre la température Te500 de l’air environnant la parcelle à l’altitude 500 hPa
et la température Tp500 de la parcelle d’air considérée :
Les modèles numériques les plus récents calculent encore d’autres index, tels que la MUCAPE (pour Most Usable Convective Available Potential Energy ) , mais à notre niveau de météorologistes amateurs, nous pourrons nous contenter d’interpréter les cartes des modèles donnant les index L I et CAPE .
Les clés pour faire une interprétation correcte sont données dans le tableau ci-dessous :
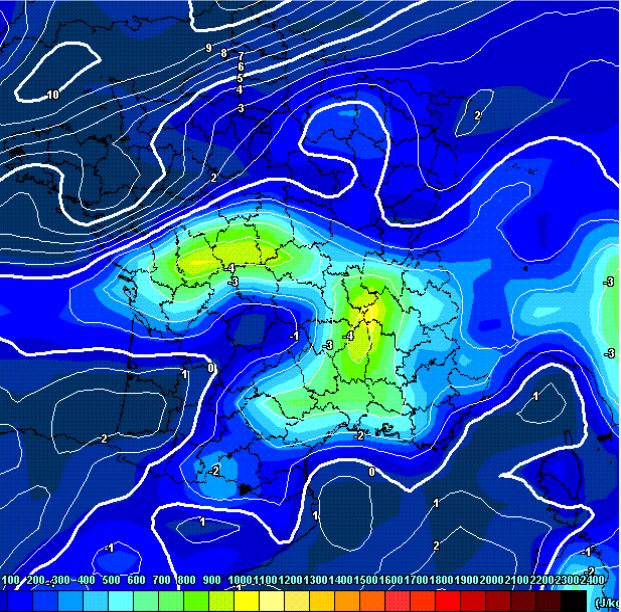
Voici ci-dessous un exemple de carte donnant la CAPE et le Lift Index LI , ici pour le 25 mai 2010 .
On voit le Lift Index L I atteint de fortes valeurs négatives allant jusqu’à − 6 °C , et cela sur une zone de plusieurs départements .
Le coloriage donne la CAPE (énergie totale potentiellement disponible pour un orage). Tant qu’on est dans le bleu foncé, pas de risque
Un orage se formera si on a À LA FOIS les deux conditions suivantes réunies : CAPE > 300 J/kg et L.I < 0
Ce qui fut bien le cas dans l’Ouest de la France ce 25 mai 2010, avec des CAPE dépassant 600 Joules / kg.
Par contre, pour ce qui concerne la prévision citée pour le vendredi 13 mars 2015, le bulletin publié s’est avéré trop pessimiste, car la sortie modèle ci – dessous est assez rassurante :
À seulement 30 heures de l’échéance, MUCAPE , une version améliorée de la CAPE standard ne présente guère de valeurs suffisantes. Mais surtout, elle n’est pas confortée par le Lift Index qui n’est nulle part négatif.
Pronostic : Il n’y aura pas d’orage ce vendredi 13 mars 2015 en fin de soirée .
* * * * *